Many biochemical processes in living cells are regulated by the concentration of free calcium ions (Ca²⁺), from contraction of muscle fibers to secretion, proliferation and cellular death. Such processes are activated by widely different concentrations of Ca²⁺, from fractions to hundreds of micromoles per litre (M).  Thus, living cells have developed powerful and sophisticated means to maintain very low basal calcium concentrations (about 0.1 M, versus a more than 10⁴ higher concentration in extracellular fluids) and to carefully regulate elevations in Ca²⁺ concentration in response to intracellular as well as extracellular stimuli. Regulatory systems range from proteins which "pump" out calcium ions by coupling this process to energy consumption or other ion fluxes, to proteic pores or "channels" – finely regulated by several possible mechanisms – in the plasmamembrane surrounding the cell; proteins are present which can bind huge amounts of Ca²⁺, and specific subcellular organelles are designed to actively store (by means of other "pumps") and release Ca²⁺ on demand (by means of other "channels").

    A composite automaton model, based on an extension of the general structure of "multilayered cellular automata", has been developed to model Ca²⁺ distribution in cellular subcompartments, taking into account: (i) the heterogeneity and spatial intertwining of the compartments; (ii) the complex regulation of Ca²⁺ transporting systems; (iii) the stochastic aspects of diffusion of Ca²⁺ and regulatory molecules and of chemical reactions.

    The general features of this model permit to tackle the simulation of the particularly complex regulation of Ca²⁺ distribution in the living cell, and of its elaborate spatial and temporal patterns. Preliminary attempts at reproducing experimental results by simulation will be presented.
 

1. General problems in modeling biological systems

    The general properties of biological systems arise from complex interactions of lower level subsystems, which can in turn be decomposed, down to the stochastic interactions among single molecules.  The first task in modeling biological systems is therefore to define the "viewpoint", i.e. the degree of detail required for an adequate description of the system.

    In particular, if modeling is aimed at gathering some insight into the mechanisms which underlie the process of interest – rather than merely reproducing the observed behaviour – the "viewpoint" will often have to be multiple, i.e. it will be necessary to simulate various aspects and subsystems at different degrees of detail and with different temporal and/or spatial resolution.  Further problems often arise in defining the simulation space, as the topological features of biological systems are in many cases complex and heterogeneous.

    These observations suggest that composite automata, endowed with the properties of parallel and local processing of information by means of mutual interactions between neighboring elements, may constitute the most appropriate framework to build efficient and accurate models of biological systems.

    Cellular automata are the best characterized local and parallel computational models. However, cellular automata in their classical form were not designed to cope with topological heterogeneity and with the coexistence of multiple subsystems and different "particle" populations. In classical applications of cellular automata, such as fluid dynamics, the cellular space [Goles et al., 1991] is homogeneous, one or a few types of particles exist, interactions among particles are mostly limited to collision, and neighborhood rules govern the movement of particles. Modeling biological systems willl require introducing the representation of several different types of elements and the specific reactions among such elements, as well as the differential diffusion of the mobile species.  To this purpose, it can be convenient to split the two aspects of reaction and diffusion, moving to more complex computational models.

    The concept of "hypercellular automata", or multilayered cellular automata, has recently been proposed by [Bandini, 1995] and [Bandini et al., 1996], as a particular case of multilayered automata network. A hierarchical structure is defined through a hypergraph, i.e. a graph composed by vertices and arcs, where each vertex is in turn a hypergraph. The multilayered automata network is directly obtained from this structure by introducing status attributes and transition functions.  Two-level multilayered cellular automata have been developed and employed to model biological systems: the first level constitutes a bidimensional cellular space (diffusion space), while at the second level a totally connected graph corresponds to each cell (first-level vertex) to generate an intrinsically parallel and local reaction space.

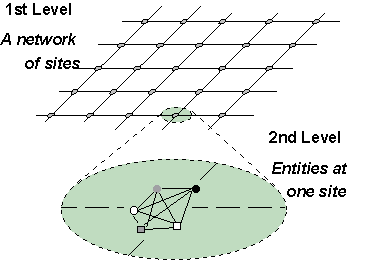
    The dynamical evolution of a multilayered automata network can be sequential, synchronous or combined.  For the biological systems faced so far, a combined procedure appeared the most convenient, i.e. updating by the alternate synchronous application of reaction rules or of diffusion rules. Reaction rules dictate status changes. The status of each entity (actor) is the set of values denoting specific attributes associated to it in order to determine its properties and behaviour; such status is changed (reaction) based on the status of all the other entities momentarily present in the same cell; thus, these rules apply to the totally connected graphs which correspond, at the second level of the hypergraph, to single first level sites. Diffusion rules determine the diffusion of entities on the cellular space. They operate on the first-level cellular space to possibly displace the entities from the site where they are momentarily located to one of the neighboring sites.

    Modeling a complex biological system entails a series of further complications, such as  heterogeneous topological domains (compartments), differential constraints to diffusion, delays in the response of specific agents or subsystems to specific stimuli, and the need to simulate different aspects (or subsystems) with different temporal/spatial resolution.

    The purpose of this work is to describe the implementation of a composite automaton,  which has evolved from hypercellular-automata models of reaction-diffusion systems, to model the distribution of calcium ions (Ca²⁺) in the subcompartments of a living cell.

2. Modeling calcium ion distribution in the cell.

    Many biochemical processes in living cells are regulated by the concentration of free calcium ions (Ca²⁺), from contraction of muscle fibres to secretion, proliferation and cellular death. Such processes are activated by widely different concentrations of Ca²⁺, from fractions to hundreds of micromoles per litre (M).  Thus, living cells have developed powerful and sophisticated means to maintain very low basal calcium concentrations (about 0.1 M, versus a more than 10⁴ higher concentration in extracellular fluids) and to carefully regulate elevations in Ca²⁺ concentration in response to intracellular as well as extracellular stimuli.
 

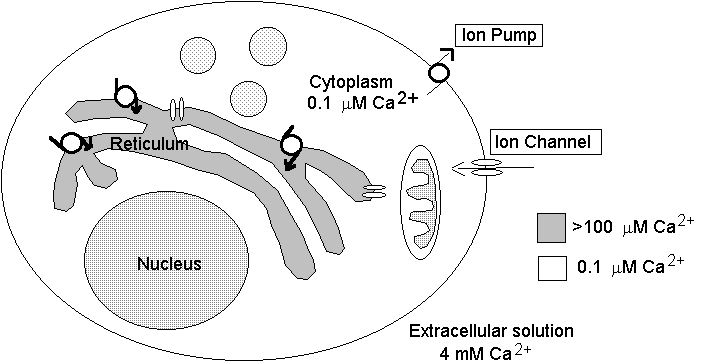
    Regulatory systems range from proteins which "pump" out calcium ions by coupling this process to energy consumption or other ion fluxes, to proteic pores or "channels" – finely regulated by several possible mechanisms – in the plasmamembrane surrounding the cell; proteins are present which can bind huge amounts of Ca²⁺, and specific subcellular organelles are designed to actively store (by means of other "pumps") and release Ca²⁺ on demand (by means of other "channels"). Such a multifarious and complex regulation, over more than 3 decades of Ca²⁺ concentration, raises some modeling problems:

• a classical representation of calcium ions as single particles would require up to about 10⁶ particles per m³ of simulated cell volume (the size of an average cell is about 500 m³), and a lattice-gas-type automaton would require about as many nodes (over 10 million for a two-dimension thin section of an average cell); furthermore, to obtain a reasonable diffusion speed for particles the simulation time step should be in the order of microseconds; on the other hand, molecular simulation of calcium ions is somehow required to reproduce stochastic fluctuations in calcium-regulated processes
• the Ca²⁺ regulation system, like most biological systems, is comprized of multiple biochemical subsystems where many different elements interact in various ways; therefore, the model must be able to host several different species of "particles", and each such element must play its role as an actor on stage
• for many sub-systems, rates and modulatory mechanisms are reasonably well characterized; therefore, although this is in contradiction with the need for low-level molecular simulation, it would be very convenient to directly introduce such knowledge as high-level rules in the simulation system.

    However, at least two problems call for specific solutions:

• species which are present at high concentrations (many particles per node) should be looked at in terms of local concentration, rather than single particles; this entails defining specific approaches to simulate diffusion of such species as well as their molecular interaction with other elements, preserving the stochastic aspects of such phenomena
• several different compartments must be defined in the simulation area (cellular space); diffusion across boundaries must be prevented, or differentially regulated by transport mechanisms; this again requires a specific approach to diffusion; furthermore, in a bidimensional cellular space, where two compartments cross each other a discontinuity arises in at least one of them, which makes bidimensional mapping inadequate for multicompartmental models.

    In order to tackle these challenges, a composite automaton has been implemented by introducing three main features in addition to the properties described above for two-layered reaction-diffusion hypercellular automata.

a. Collective actors

    The composite automaton is based on a cellular space simulating the living cell; objects endowed with status attributes simulate chemical substances present in the living cell, and will be called "actors"; actors can move to neighboring cells according to diffusion rules and can react with other actors momentarily present in the same cell according to reaction rules (which change status attributes).  Calcium ions, which may be present at high concentrations (up to >100 per cell), are not considered singularly. Rather, collective actors are introduced in the automaton; such collective actors have a fixed location, are present in all cells where Ca²⁺ can occur, and have a status attribute dedicated to represent the number of Ca ions momentarily present in the cell. Single Ca ions are represented by bits in a fixed-length string, the concentration attribute, which is randomly scrambled at each step in the life of the system; Ca²⁺ concentration will intervene in any reaction which is influenced by Ca²⁺, by means of string-matching operations on the concentration string. This ensures that Ca²⁺-dependence of any process is modeled even in its stochastic aspects.  Thus, the function of collective actors is to increase the resolution of the model down to the molecular level, without concurrently requiring shorter time steps and a finer spatial grid; they constitute the "underground" portion of the model, working like lower-level automata.

b. Cellular space and compartments

    The existence of different compartments is handled by assigning each element in the cellular space to a specific compartment (e.g. extracellular, cytoplasm, intracellular organelles, endoplasmic reticulum). Specific status fields will determine which compartments each actor can reside in. In general, barriers to diffusion will exist at boundaries between cells belonging to different compartments; however, specific status attributes may endow actors with the capacity, or possibly the duty, of crossing such boundaries.  Conversely, diffusion will generally be free among cells belonging to the same compartments.

    All this profoundly affects the fundamental properties of the cellular space, which becomes a graph where different kinds of vertices and arcs are allowed (i.e. different compartments and direct connection or different boundaries between cells).

    A further generalization with respect to classical cellular space is introduced in the automaton to cope with the limitations arising from a bidimensional simulation area: the cellular space is created as a graph where each vertex (cell) is connected to at least four other vertices, by means of arcs of possibly different kinds (depending on the compartments the two connected cells belong to). A subpopulation of the vertices and arcs map, respectively, to cells in a bidimensional simulation area and to the neighborhood relations among such cells; this makes it possible to display a representation of the simulation area. The other vertices map to cells outside the bidimensional simulation area and provide – together with the arcs originating from them – (i) the continuity when two compartments cross each other and (ii) a virtual extension of the bidimensional simulation area where this has to be arbitrarily truncated.

c. The rules

    In addition to the main sets of rules mentioned above, i.e. reaction and diffusion rules, which we may more appropriately call molecular reaction/diffusion rules, the automaton contains two further sets of rules, which govern collective reaction and diffusion.

• Molecular diffusion rules apply to all mobile actors; they govern the movement from a site to one of the neighboring sites (be they inside or outside the displayable bidimensional area). For each actor in each location, the applicable rules are directly determined by the status attributes of the actors, by the type of the cell and by its neighborhood relations (i.e. by the type of the corresponding vertex and of the arcs originating from it): in other words, the diffusion rule A-C-C' determines how an actor with diffusion attribute A which is located in a cell of a specific compartment C can move to a neighboring cell, belonging to compartment C'.
• Reaction rules apply to all actors, simple as well as collective ones; reactions occur according to a totally-connected-graph scheme, i.e. they involve, for each cell, all actors momentarily present that particular cell. However, reaction fields in the structure of each actor determine, by means of string-matching rules, the other actors they can significantly interact with. Object oriented programming makes it easy to create methods for each actor which produce the desired changes in status attributes following recognition of a matching actor. Self reaction is also allowed to reproduce delays (countdown in a specific field) and complex responses (stepping through a series of states).
• Collective reaction rules are just a subclass of reaction rules, with the exception that they do not apply to the totally connected graph of actors simultaneously present in the same cell, but rather on a reduced graph where each collective actor is connected to all other actors in the cell which possess the appropriate matching string. These rules are generally more complex than molecular reaction rules in that string matching of the concentration attribute to appropriate strings presented by the counterpart can determine graded changes in specific status attributes, thereby simulating graded activation/inactivation of proteins and mechanisms as functions of Ca²⁺ concentration, preserving in the mean time the stochastic aspects of molecular interactions. Reactions between collective actors are allowed to simulate, for example, the binding/unbinding of calcium-ions to Ca²⁺-buffering proteins, through the comparison of the concentration strings of collective actors which respectively represent the populations of free and bound calcium ions in the cell. This simulates slowing down of Ca²⁺ diffusion by the buffering proteins.
• Collective diffusion rules apply to collective actors only, and in particular to collective actors located in adjacent cells. Adjacency between two cells for collective diffusion is determined by the existence of permissive arcs between the two vertices that represent the two cells, in the graph which defines the simulation space. These rules consist in the swapping of variable length substrings between the concentration attributes of the two involved collective actors, and simulate the movement (diffusion) of particles present at high concentration, by means of changes in status attributes, rather than location, of specific actors. Thus, as we shall shortly see, these rules must be formally distinguished from both reaction and molecular diffusion rules.

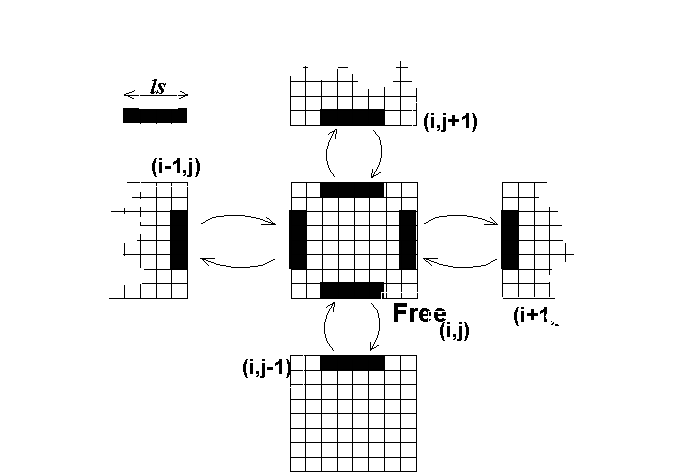
    Let us indicate by DM and DC the procedures to update the system by applying the molecular diffusion rules and the collective diffusion rules, respectively, and by RM and RC the procedure to update the system by applying the molecular and collective reaction rules, respectively. Let us also indicate by G₀ the graph where each vertex correspnds to a cell in the simulation space and the arcs define the neighborhood relations, and by G_i {i =1,N} –  where N is the total number of vertices of G₀ – the totally connected graph dynamically generated at each step by the set of actors momentarily present in the cell mapped by vertex i of G₀.

    We can observe that RM and RC are formally similar, in that they apply to  G_i {i=1,N} and work independently for each cell, i.e. the execution of these procedures on the whole system is exactly equivalent to the parallel execution of the same rules on each single cell of the automaton. Furthermore, the execution of RM and RC do not produce any displacement of actors in the simulation space but only changes in the status attributes.

    Conversely, execution of the DM procedure is exactly equivalent to the parallel application of molecular diffusion rules to each single mobile actor.  This procedure brings about changes in the location of actors in the simulation space but does not affect any status attribute.

    This reproduces the two-step updating procedure of a reaction-diffusion hypercellular automaton, where the two steps apply to two different domains – i.e. the cohort of actors for the diffusion step and the set of cells for the reaction step.

    Execution of the DC procedure, finally, applies to a third, different domain, because it is equivalent to the parallel application of the corresponding rules to each arc in G₀. Furthermore, it simulates the diffusion of elements, present at high concentration in the system, by affecting the status of collective actors, i.e. it simulates diffusion but is formally equivalent to a reaction step (albeit the reacting actors are present in adjacent cells rather than in the same one).

4. Notes on the implementation

a) The user interface

    The model is set up by the user who defines G0, starting from a graphical representation of the bidimensional displayable space (possibly mapped on a digitized micrograph obtained experimentally from a living cell) and adding "external" cells where needed to grant the continuity of intersecting compartments.

    The initial population of actors is generated and their initial location and set of status attributes are defined.  This procedure can be performed, at will, either on the whole simulation area (independently for each compartment) or on selected regions or single cells. The parameters of most reactions can be set to default values or tuned at will.

    When the simulation starts, a window displays the simulation area: a color code represents local calcium concentrations and the location of selected actors can be displayed. A second window yields full information on the actors momentarily present in a chosen cell, and lets the user modify their attributes. A control window lets the user suspend/restart the execution, select the monitored area and cell, change the number of actors and define the mode for data saving: time courses of relevant status attributes of specific actors, time courses of average Ca²⁺ concentration and transcompartmental fluxes, in the selected area, can be saved; images of local Ca²⁺ concentration can be saved at the desired time intervals.

b) The actors

    Actors are present in the model to represent each relevant biological aspect. An actor does not necessarily correspond to a biological entity (see, below, collective actors and shuttles).

    Each actor is a software object containing (i) a series of status attributes, (ii) a binary string which determines, by means of boolean operations, which other actors it can interact with, and (iii) all the procedures aimed at changing its status attributes as a consequence of the interaction with other actors (reaction rules).  Most status fields regard the "functional state" of the actor, and its behavior in reaction procedures.  Diffusive behavior is affected by an access field which defines the compartments the actor can reside in and move to, and by a direction fields which determines whether the actor is fixed or, in case it is mobile, whether diffusion is random or along an assigned direction (this permits the deterministic translocation of actors).

    The main classes of actors are collective actors, carrier actors and  mobile actors.

    Collective actors –  called Free and Bound – are fixed and represent calcium concentrations in the cell they are located in, by means of a binary string – the concentration string – where each set bit represents a fixed number of calcium atoms (1 in the cytoplasm, about 100 in compartments where calcium concentrations are higher).  Ca²⁺ diffusion within each cell is simulated by shuffling Free's binary string, Ca²⁺ binding/unbinding is simulated by transferring bits from suitable length substrings in Free to Bound and viceversa, and diffusion to neighboring cells is simulated by swapping fixed length substrings with Free actors in the neighboring cells. The occupancy of Ca²⁺ receptors and the degree of activation of Ca²⁺-dependent processes are easily defined by reaction rules which look up the number of set bits in substrings from the concentration string of either Free or Bound.

    Carrier actors simulate Ca²⁺ channels and pumps. They are located in cytoplasmic cells confining with other compartments, and they are in particular associated with a single arc in G₀ which connects two vertices of different kind. These actors simulate the opening of a pore or the active transport of calcium ions in a graded fashion, depending on their status. This allows for any kind of complex regulation of such mechanisms. The actual translocation of calcium ions is performed by shuttle actors, which are generated with the appropriate capacity and released into the cell; shuttles are loaded with Ca²⁺ by reacting with Free and mandatorily migrate along the appropriate arc of G0 for a defined number of steps (usually 1 or 2, i.e. back and forth).

    Mobile actors simulate any diffusible biological entity of interest – mostly regulatory molecules – which can be generated by specific reactions and in turn react with specific actors. They usually have a life field in their status which limits in time their persistence in the automaton. They may exhibit access restrictions to the different compartments and mqy diffuse either at random or along obligatory directions (see the description of the shuttles above).

c) Algorithms and boolean operations on status strings

    A series of algorithms have been developed to appropriately simulate diffusion and complex dependence on Ca²⁺ concentration.  Based on experimentally determined chemical-physical parameters and on theoretical computations, the probability of a particle leaving a fixed-volume cell during a fixed-duration time step in any direction is computed, thereby fixing the probability for a mobile actor to be displaced from its current location and the extent of the substring in Free's concentration attribute to be swapped with neighboring Frees. Based on the knowledge of the affinity for Ca²⁺ of the binding proteins and of other Ca²⁺ receptors, the momentary occupancy of the latter is determined by boolean operations on substrings of Bound's concentration attribute. Boolean operations on substrings of Free's concentration attribute also reproduce polynomial approximations to high-order functions that describe the dependence of specific functions on Ca²⁺ concentration.

Conclusion

    The model here described to simulate the dynamic regulation of Ca2+ distribution in the subcompartments of a living cell constitutes a novel implementation of a composite computational automaton, based on an extension of reaction-diffusion hypercellular automata.

    The basic structure of a cellular automaton for the simulation of diffusion is extended by introducing different kinds of particles and a second layer of totally connected graphs to simulate local and parallel reaction among the particles (hypercellular automaton).

    The hypercellular automaton, where diffusion rules operate on the vertices of lower-level graph (cells) and reaction rules operate on the corresponding set of second-level graphs, is further extended by introducing (i) the existence of different kinds of cells and restricted diffusion in the first-level graph, (ii) a set of updating rules that operate on the arcs of the first-level graph and (iii) particles that are de facto automata themselves. The latter make it possible to reproduce underlying molecular processes whose simulation would require a finer spatial/temporal resolution.

    The general features of this model permit to tackle the simulation of the particularly complex regulation of Ca²⁺ distribution in the living cell. Most problems here discussed also occur in their general features in other complex biological systems, where many different agents are present, several compartments must be considered, different degrees of detail are required in the simulation of different aspects, and high order functions describe the dependence of certain functions on regulatory factors. It appears therefore that the composite automaton here presented offers a general scheme which should make many apparently untractable biological processes amenable to computer simulation.