from: Philosophiocal transactions of the Royal Society (London)
Biological Sciences, volume 354: pages 319-329, 1999.
[A special issue on "Molecular and cellular aspects of exocytosis]

THE KINETICS OF NERVE-EVOKED QUANTAL SECRETION 

Riccardo Fesce
CNR Center of  Cytopharmacology and Dibit, Dept. Neurosciences, S. Raffaele Scient. Inst.
via Olgettina 58, 20132 Milano - Italy 
SUMMARY
Current views on quantal release of neurotransmitters hold that after the vesicle migrates towards release sites (active zones) multiple protein interactions mediate the docking of the vesicle to the presynaptic membrane and the formation of a multimolecular protein complex (the "fusion machine") which ultimately makes the vesicle competent to release a quantum in response to the action potential. Classical biophysical studies of quantal release have modeled the process by a binomial system where n vesicles (sites) competent for exocytosis release a quantum, with probability p, in response to the action potential. This is likely to be an oversimplified model; furthermore, statistical and kinetic studies have given results which are difficult to reconcile within this framework.
Here, data are presented and discussed which suggest a revision of the biophysical model. Transient silencing of release is shown to occur following the pulse of synchronous transmitter release which is evoked by the presynaptic action potential. This points to a schema where the vesicle fusion complex assembly is a reversible stochastic process. Asynchronous exocytosis may occur at several intermediate stages in the process, along paths which may be differentially regulated by divalent cations or other factors. The fusion complex becomes competent for synchronous release (armed vesicles) only at appropriately organized sites. The action potential then triggers (deterministic-ally rather than stochastically) the synchronous discharge of all armed vesicles.
The existence of a specific conformation for the fusion complex to be competent for synchronous evoked fusion reconciles statistical and kinetic results during repetitive stimulation, and helps explaining the specific effects of toxins and genetic manipulation on the synchronization of release in response to an action potential. 
INTRODUCTION
It is generally accepted that quantal release of neurotransmitters involves exocytotic fusion of synaptic vesicles (Ceccarelli and Hurlbut, 1980). During intense activation of quantal secretion synaptic vesicles undergo multiple cycles of exo-endocytosis. Although the precise sequence of events has not been fully clarified, it is generally agreed that vesicles may be mobilized from a reserve pool - vesicles reversibly associated to the actin-based cytoskeleton of the nerve terminal through the membrane-associated phosphoprotein synapsin I - and cluster near specialized sites on the presynaptic membrane (active zones). Here, the specific interaction among vesicle-membrane proteins (synaptobrevin, synaptotagmin), soluble factors (N-ethylmaleimide-sensitive fusion protein or NSF, soluble NSF attachment protein or SNAP, and other modulatory proteins) and plasmalemmal proteins (syntaxins, synaptosome associated protein 25 or SNAP-25, calcium channels) promotes the formation of a multimolecular complex (SNAP receptor protein complex or SNARE complex) which mediates exocytotic fusion (Calakos and Sheller, 1996; Hanson et al., 1997). The vesicle membrane may then be retrieved on the spot (Ceccarelli et al., 1973; Fesce et al., 1994; Palfrey and Artalejo, 1998) or via coated pits and coated vesicles (Heuser and Reese, 1973; Cremona and De Camilli, 1997).
Morphologically, some vesicles appear in close contact with the presynaptic membrane at the active zones ("docked" vesicles). However, the precise molecular features of vesicle docking are not clear. Attempts have been performed at defining whether each protein involved in exocytosis comes into play before or after docking, and vesicles ready for exocytosis have sometimes been indicated as "cocked" - or docked and competent for release. The term "readily releasable quanta" has also been used in the literature; this implicitly suggests that vesicles appropriately positioned and primed by protein interactions might undergo spontaneous exocytosis and also display a defined probability of releasing their quantum in response to the action potential.
Actually, no precise functional meaning can be attributed to any of these terms.  In particular, competence for fusion has been evaluated using several different means of stimulation - hypertonic solutions, elevated K+, toxins, drugs or electrical stimulation - although no evidence is available to indicate that the various treatments act on the same vesicle conformation(s) and population(s).
Here we shall discuss how the concurrent analysis of asynchronous quantal release and synchronous release evoked by the presynaptic action potential might help in dissecting functionally defined stages in the exocytotic cycle, based on the statistical and kinetic properties of the secretory activity.

1. Approaches to statistical and kinetic analysis of quantal release
The history of electrophysiology of quantal release is half a century long. During these decades, the initial hope that the mechanisms of transmitter release and the properties of the synaptic secretory machinery might be clarified and understood by means of quantitative statistical and kinetic analysis of postsynaptic responses has gradually surrendered to the ever growing awareness of the complexity of transmitter release modulation by a multitude of functional, biochemical and pharmacological factors.
A classical approach to the study of quantal release has been the statistical analysis of fluctuations in quantal content of synaptic responses evoked by presynaptic stimulation at low frequency. The statistics of quantal content in successive responses to electrical stimulation can be described by binomial statistics at many synapses, and this has suggested that a defined number n of entities (be they releasable vesicles, release sites or active zones) can produce the release of a quantum of transmitter, with probability p, in response to a presynaptic stimulus. However, estimated values and changes of n and p under various experimental conditions could not be easily reconciled with a comprehensive and consistent interpretation. Most difficulties in this approach presumably arise from the unreliability of the estimated binomial parameters, in the presence of heterogeneous probability of release and temporal variability during repetitive stimulation, which cannot be spotted by standard binomial analysis but markedly affect the estimates (see Brown et al. 1976). Although these problems might in principle be overcome by more sophisticated approaches to statistical analysis of quantal content (Courtney, 1978; Miyamoto, 1986;  Fesce, 1990), this path has not been systematically explored.
A conceptually different, kinetic approach was also employed in investigating the question: the probability of release was estimated from the decrease in endplate potential (EPP) amplitude (or in quantal content) in response to pairs or trains of stimuli delivered at short intervals (Liley and North, 1953, Thies, 1965;  Elmqvist and Quastel, 1965). Mallart and Martin (1967) combined the regression of quantal content on total past release with ensemble averaging over several trains of stimuli, to reduce fluctuations and increase the reliability of the approach. In the absence of recycling (i.e. at sufficiently short intervals between successive stimuli) the fractional decrease in quantal content between the stimuli should reflect the fraction of available quanta released (or release sites activated) by the first stimulus - i.e. p - and the regression of quantal content (m = n × p) on total past release (which should parallel the decrease in n, in the absence of recycling) should also yield an estimate of p. Although this approach seemed self-evident, a series of undemonstrated (or even false) assumptions were implicit in it: even accepting that n entities with probability p of determining release of a quantum are sufficient to describe the system and no recycling occurs in short time intervals, no evidence indicates that p will remain unaltered between successive stimuli. Indeed, Betz (1970) and Christensen & Martin (1970) demonstrated that the decrease in quantal content of the second EPP is not linearly but rather quadratically related to the size of the first EPP, thereby suggesting that p is decreased to about the same extent as n, as a consequence of release in response to the first stimulus; the authors proposed that preferential release of high-probability quanta in response to the first stimulus might explain this finding. However, it  appears that this approach also is unable to yield clear-cut and consistent answers to the question of what statistical and kinetic parameters determine the quantal content of evoked responses. 



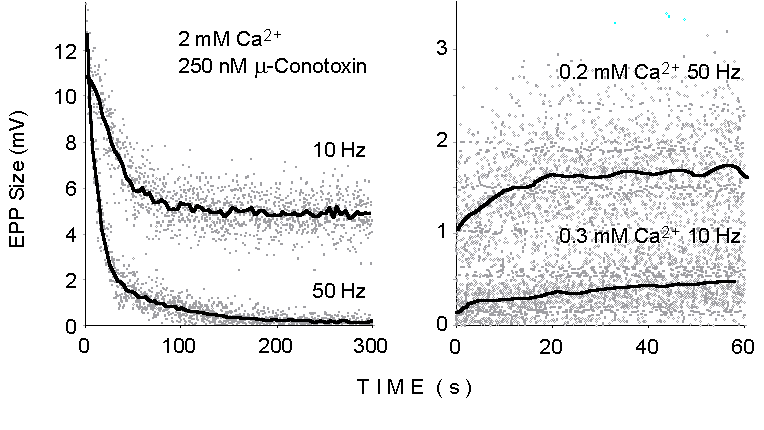
Figure 1. The dots illustrate the peak size of successive EPPs recorded at motor endplates in the mouse extensor digitorum longus (EDL) muscle during trains of stimuli delivered to the sciatic nerve at various stimulation frequencies and under the different experimental conditions indicated. The lines display momentary average values smoothed over time. 250 nM mu-Conotoxin added at normal Ca2+ concentration (2 mM; left panel) to prevent muscle action potential and twitching.

2. Binomial analysis during sustained electrical stimulation
At the neuromuscular junction, markedly heterogeneous time courses can be induced in EPP size and quantal content by repetitive stimulation at relatively high frequency (10-100 Hz). Figure 1 illustrates the declining responses observed during repetitive stimulation at 10 and 50 Hz in physiological extracellular Ca2+ concentration (Left: 2 mM Ca2+, 250 nM mu-Conotoxin added to prevent muscle action potential) and the growing responses at lowered Ca2+ concentrations (Right: 10 Hz, 0.3 mM Ca2+; 50 Hz, 0.2 mM Ca2+). Such changes reflect the dynamic balance between synaptic facilitation and potentiation processes on the one hand and synaptic depression or vesicle depletion on the other. Spontaneous quantal release can be measured by counting the mEPPs which occur between pairs of successive stimuli: during repetitive stimulation asynchronous release is also affected by facilitation and depression processes. However, asynchronous and evoked quantal release are known to be differentially regulated by Ca2+ and other divalent ions and dissimilarly affected by drugs and toxins. Figure 2 shows that also repetitive stimulation produces differential effects on evoked and asynchronous release: initial facilitation phenomena are markedly more evident in mEPP rate than in EPP size, whereas profound depression of evoked, but not asynchronous, release is apparent at late times during high-frequency stimulation in normal Ca2+. 

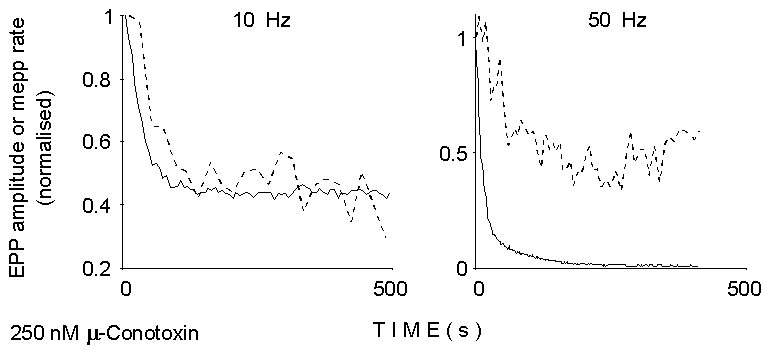0
Figure 2. Smoothed time courses of EPP size and mEPP rate of occurrence between EPPs during the two trains of stimuli illustrated in Figure 1 (left). Calcium concentration, 2 mM; 250 nM mu-Conotoxin. Notice the delay in depression of asynchronous release at 10 Hz, and the initial facilitation and less prominent depression at 50 Hz.

The results of binomial analysis under these experimental conditions are illustrated in Figure 3. The results are consistent with a binomial model, as they point to a limited value for the parameter n, in agreement with most previously published observations under various experimental conditions. The decrease of the n parameter during the train in normal calcium is not unexpected and may reflect quantal depletion and/or fatigue; instead, the apparent increase in n, rather than p, in low Ca2+, is puzzling, as is the decrease in p which is observed in normal Ca2+ (although previous similar analyses also suggested a concurrent decline in both n and p during repetitive stimulation which produces synaptic depression; Mallart and Martin, 1967). 


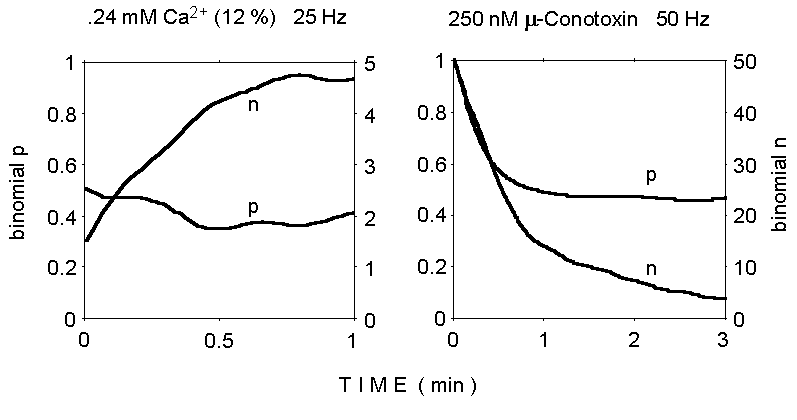
Figure 3. Binomial analysis of quantal content of EPPs during two trains of stimuli. Notice the gradual increase of binomial n from the initial very low value at reduced Ca2+ concentration (left panel), and the decrease in both n and p during stimulation at 50 Hz in normal Ca2+ concentration (2 mM; 250 nM mu-Conotoxin added; right panel). 

The main problems arising with binomial analysis are related to variability among the p values for different sites - which decreases response variance - and to variability of n and p in time - which increase response variance. Although such phenomena prevent accurate and meaningful estimates of the parameters, relative changes in the estimates during an experiment or under different experimental conditions still yield relevant information on the underlying processes.

3. Correlation analysis
Under all conditions here examined the estimates of n at late times are consistently very low (< 10). It is worth pointing out that, although estimates of n and p may be inadequate, quantal analysis yields a solid piece of information: the variance in quantal content is too low for a Poisson system (characterized by a high number of possible events occurring with very low probability). Such low variance obviously is an important positive feature in terms of information processing at the synapse, and it might be observed that both a limited number of functional release sites and heterogeneous probabilities of release are advantageous features in terms of decreased output variability.
The clear indication of a limited number of release sites was exploited in the past to try and get relevant information on the process from the analysis of successive responses in a train of high frequency stimuli. A more robust approach would be the application of autoregressive analysis to quantal contents during sustained stimulation. In particular, one could investigate the autocorrelation of EPP sizes (or quantal contents) in a reasonably stationary condition, i.e. the dependence of the size of each EPP on the size of the previous one, during prolonged stimulation. EPPs with a particularly high quantal content (due to random fluctuation) should be preferentially followed by undersized EPPs (due to larger momentary depletion). Systematic analyses by this approach should be able to validate the n × p model while yielding information on both parameters and on the time constant of the quantum reconstitution process.
A problem arises if the parameters of the secretory process change with time. In this case, oversized and undersized EPPs will tend to cluster (positive correlation of EPP sizes), reflecting changes in momentary mean values. This idea was used to investigate whether slow fluctuations in transmitter release are sustained by calcium fluctuations in the nerve terminal (Meiri and Rahamimoff, 1978). However, even though the mean EPP size may change with time, the departures of EPP sizes from the momentary mean value need not be correlated, unless the quantal content of an EPP directly influences subsequent output .
If an almost steady state can be reached, the number of quanta recovered between stimuli will balance the expected number of quanta lost (n × p). Whenever an EPP with quantal content greater than expected occurs (m > n × p) the number of quanta available for next EPP should decrease by the number of quanta released in excess (e) and quantal content should be transiently depressed (by a factor close to e × p, neglecting rapid recycling). Such an effect of random fluctuations of quantal content on subsequent responses should be detectable if n is small (and thereby significantly affected by small changes in quantal release) and should fade away with the time constant of quantum reconstitution. In other words, the autocorrelation of the departures of quantal content from its momentary mean value should pinpoint the memory of the system.
More precisely, let nj be the number of activatable sites at stimulus j, and pj the corresponding probability of release. The expected quantal content is E[mj] = nj × pj. For a constant p and in the absence of recycling, we would have nj+1 = n0 - SUM[m0, m1, m2 ... mj], and E[mj+1] = (n0 - SUM[m0, m1, m2 ... mj]) × p. Thus, -p would be the slope of quantal content versus cumulative previous release (Elmqvist and Quastel, 1965). If rj  quanta are refilled between stimuli j and j+1, the available sites at stimulus j+1 will be nj+1 = nj - mj + rj . Thus, the next expected quantal content will be E[mj+1] = (nj - mj + rj) × pj+1.  If the stimulation proceeds until a steady state is reached, p will become constant and the average values of m (<m>) and of r (<r>) should become equal (release equals refilling).
Thus, at steady state,  E[mj +1 - m] = (nj - mj + rj) × p - m = E[mj - m] - (mj - rj) × p
and   E[(mj+1 - <m>) - (1 - p) × (mj - <m>)] = (rj - <r>) × p.
If the departures of r from its mean value are random, this equation defines a first order autoregressive system, so that simple mathematical processing of the autocorrelation of fluctuations in quantal content at steady state should yield a value for p. In particular, the autocorrelation of quantal content should display the behavior illustrated in Figure 4A. However, if the recycling/refilling speed were highly correlated with quantal content (i.e. most of the quanta released in response to a stimulus are rapidly reconstituted before next stimulus), then no correlation should be detectable. 



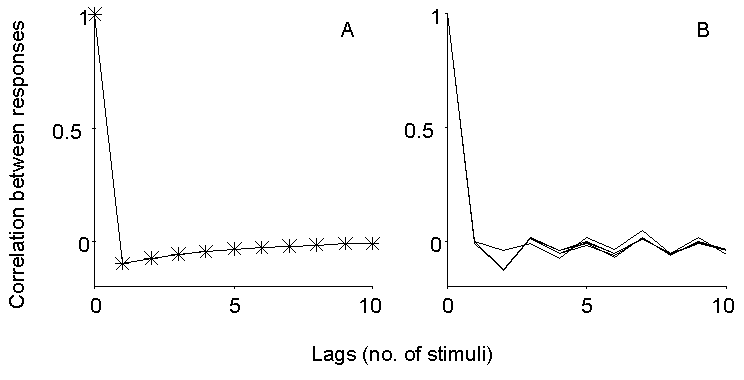
Figure 4. Expected and observed autocorrelation of EPP size fluctuations during repetitive stimulation. Left panel illustrates the expected behavior for low n and transient depression following oversized EPPs (see text). The right panel shows the autocorrelation computed at late times during trains of stimuli at 10 and 50 Hz in 2 mM Ca2+ and 250 nM mu-Conotoxin, at 25 and 50 Hz in 0.3 mM Ca2+ (15%) and at 100 Hz in 0.24 mM Ca2+ (12%). No consistent autocorrelation is observed on the fast time scale here considered, and in particular no undershoot is observed for lag=1, as would instead be expected for a small pool of quanta subject to momentary depletion.


Actually, one may ask why such an approach has not been previously applied at all. The answer is probably a simple one: negative results never get published. In fact, no dependence of EPP quantal content on the size of previous EPPs could be detected at the mouse EDL muscle during repetitive stimulation, at frequencies from 10 to 100 Hz and under conditions of depressed as well as normal quantal content. Figure 4B illustrates the autocorrelation of EPP sizes at steady state during trains of stimuli in normal Ca2+ (250 nM mu-Conotoxin) at 10 or 50 Hz, and in reduced Ca2+ concentration (0.3 mM, 25 or 50 Hz; 0.24 mM, 100 Hz). No significant correlation could be detected under any of these conditions, although inconsistent fluctuations on a longer time scale were often apparent.
If momentary depletion occurred after each stimulus, and its extent were related to recent quantal output, negative correlation should arise between EPP size and mEPP frequency between successive stimuli. Again, as shown in Figure 5, no significant autocorrelation could be detected for either EPPs or mEPPs and no cross-correlation was apparent between EPPs and mEPPs. These results are difficult to reconcile with a binomial model, considering in particular that estimates of n at steady state are quite small (< 10) for the repetitive stimulation protocols examined here.


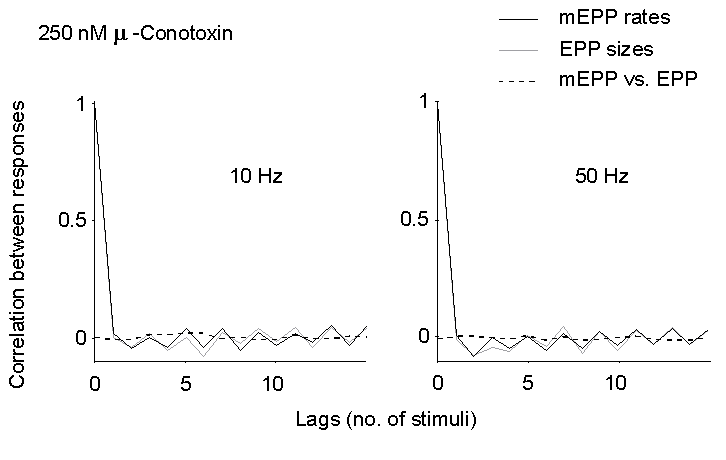
Figure 5. Autocorrelation of EPP size and mEPP rate of occurrence (between EPPs), and cross-correlation of mEPP rate vs. EPP size at late times during trains of stimuli in 2 mM Ca2+ and 250 nM mu-Conotoxin. No significant correlation can be detected, either at 10 or 50 Hz. 

4. Is a binomial model (and a statistical model in general) of any usefulness ?
Even though statistical and kinetic analysis of quantal content are unable to yield a consistent dynamic model of the release machinery, the conceptual framework of binomial statistics is helpful in considering the features of information processing at the synapse. An optimally designed synapse, in terms of consistency of information processing, should display both low variability under stationary conditions and no memory of past output (and especially of its random fluctuations) under repetitive stimulation. If one were to choose a statistical system for quantal release such that error (and variability) is kept to a minimum, a limited number of release sites with high probability of releasing a quantum would fit best, and quantal contents would obey binomial statistics with finite n, as observed distributions at rest usually do; on the other hand, such a system would be affected by correlation between successive events (occasional oversized responses would significantly depress subsequent release) whereas an unlimited number of release sites with very low release probability (a Poisson system) would be best to grant the observed independence.
Thus, simple models may be inadequate to describe the synaptic release machinery, which is endowed with a particularly favorable behavior: it is characterized by low variability (high reliability) under basal conditions; it can be modulated by activity over a wide range of efficiency levels; still, it is sufficiently memoriless not to be affected by random fluctuations in its own previous output (low correlation and again high reliability).
An intriguing perspective which has not been investigated in detail regards the possibility that release may actually produce a momentary depression of activated release sites, but refilling of the active sites (or of a readily releasable pool of vesicles) might be so fast that the momentary depletion which follows a release event is rapidly recovered from before the next stimulus arrives, and no correlation between successive responses can be observed.

5. Recovery between stimuli
Alternative hypotheses can be put forward to explain the lack of correlation between successive EPPs at steady state: release sites might be loaded with more than one releasable quantum although they release only one at a time; the number of quanta and/or release sites might be so high that the number of quanta released with any single EPP cannot noticeably affect the release machinery (although this is in contradiction with the low values for n consistently reported in the literature).
In order to investigate these possibilities neuromuscular junctions were subjected to "random interval" stimulation, i.e. repetitive stimulation at variable time intervals, with mean stimulation rates of 10-20 Hz. The analysis of a representative experiment is illustrated in Figure 6. Here, the average interval between stimuli was 67 ms (15 Hz) and extracellular Ca2+ concentration was 0.4 mM. The average EPP sizes (groups of 166 successive EPPs) are plotted on the left as a function of time, to illustrate the overall time course of release. On the right, the departures of EPP sizes from the momentary average were computed and the values were grouped according to the time interval between the corresponding stimulus and the previous one. The decaying facilitation is apparent from the smooth curve (two-exponential decay with time constants about 10 and 70 ms).  However, at short time intervals the data depart from the exponential decay fit to the data, suggesting an initial depression which fades away with a time constant of  about 6 ms. 



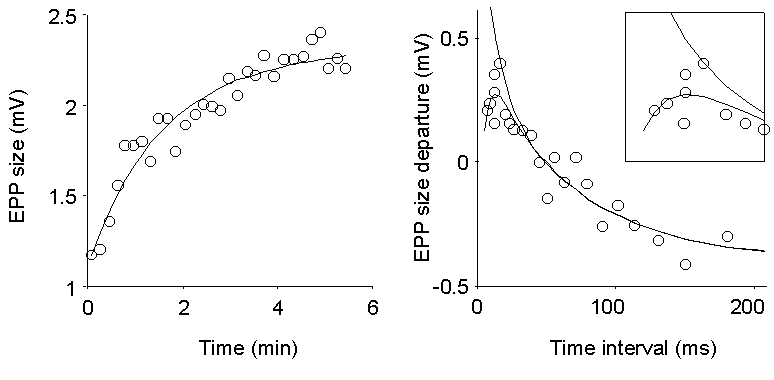
Figure 6. Analysis of EPP sizes during stimulation at random time intervals. Mean stimulation frequency, 15 Hz;  0.4 mM Ca2+ (20%).  Left panel shows successive averages of groups of 166 EPPs and a smooth analytical fit to the overall time course (two-exponential rise with time constants of 75 and 175 s, respectively). Right panel displays the departures of EPP sizes from the momentary average; each point represents 100 EPPs, grouped according to the time interval which precedes the corresponding stimulus. The smooth decaying indicates facilitation which decreases as the interval gets longer. It is well fit by a two-exponential decay with time constants of 68 and 9.8 ms, respectively. For short intervals, the points fall below the fit, indicating an initial depression, which vanishes with a 6.5 ms time constant (see also inset).

This suggests that a momentary depletion of releasable quanta (or silencing of release sites) does occur after each episode of evoked release, although recovery is so rapid (within 10-20 ms) that no "memory" of recent output is detected for stimulation rates up to 50 Hz.
In order to further investigate this point, an autoregressive deconvolution procedure (Fesce, 1990; Sacchi et al., 1998) was applied to the time course of the averaged EPPs during repetitive stimulation. Figure 7 illustrates the results of this approach for a train of stimuli at 50 Hz in normal extracellular Ca2+ concentration: the average EPP time courses are shown for the first 150 EPPs in the train and for groups of 1000 EPPs at 2 and 5 min after the onset of stimulation (upper left). The analytical shape of the mEPPs (the difference between two exponentials, fit to averaged mEPPs isolated from the same recording) was deconvolved into the average EPP waveform to yield an estimate of the probability of release as a function of time after the delivery of the stimulus (upper right). Deconvolution reveals a peaky pulse of synchronous release (for the initial oversized EPPs nonlinear summation is relevant and somewhat smoothens the peak, giving rise to an artifactual shoulder on the decay phase). The pulse of synchronous release is delayed at late times, but is over by 2 ms after the stimulus, and is followed by a tiny tail of release. The relative relevance of the tail is appreciated from the cumulative release curves (lower left) which are obtained by integrating the probability of release over time. The tail becomes more prominent at late times, in agreement with the less marked depression observed for asynchronous release (Figure 2). The cumulative release curves display a momentary flattening (particularly apparent for late EPPs) which precedes the slow asymptotically rising phase. This indicates temporary silencing of release. Inspection of the curves of release probability at high amplification (lower right) confirms this impression: the probability of release decays exponentially at times greater than 5 ms, but backward extrapolation of the decay highlights the temporary silencing that follows synchronous release, from which the synapse rapidly recovers. 


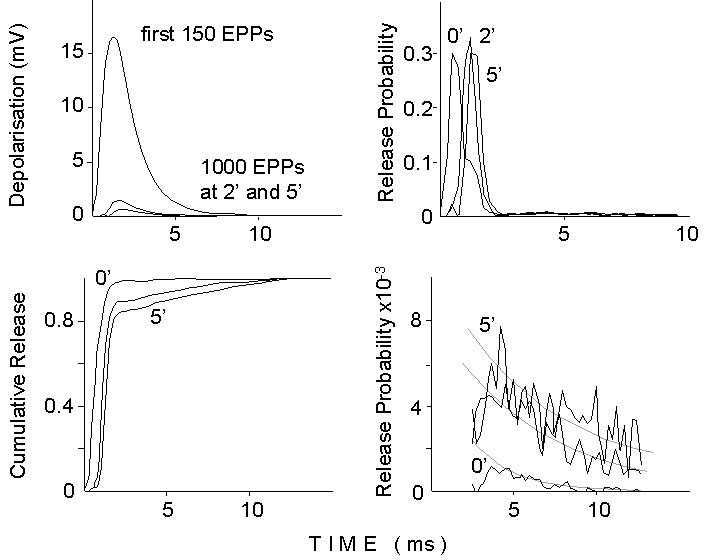
Figure 7. Deconvolution analysis of the EPP waveform during a 50 Hz train of stimuli delivered in 2 mM Ca2+ and 250 nM mu-Conotoxin. Top left: average waveform for the first 150 EPPs and for groups of 1000 EPPs at 2 and 5 minutes after the onset of the stimulation. Top right: Release probability curves obtained by deconvolving the average mEPP waveform (the difference between two exponentials with 0.6 ms rise time constant and 4 ms decay time constant) into the averaged EPP. Notice the shoulder in the deconvolution for the first group (0 min), produced by flattening of the peak, due to nonlinear summation, for the first oversized EPPs. Bottom left: cumulative release curves obtained by integrating the release probability curves. Notice momentary flattening and increasing slow component for later times. Bottom right: tails of release probability curves redisplayed at higher gain (the first 3 ms have been canceled). Notice the initial depression and the exponential decays, after 4-5 ms.

The results of random-interval stimulation and deconvolution of the EPP waveform indicate that temporary silencing of release follows synchronous secretion induced by the action potential during sustained stimulation. Paired pulse experiments at single hippocampal synapses at rest (Stevens and Wang, 1995) revealed a rapidly waning depression (about 5 ms silencing followed by recovery with a time constant of about 5 ms) at synapses where a quantum had just been released. From those experiments it could not be concluded whether such a depression would also be present (and if so, to what extent) at actively secreting synapses. The data here recalled indicate that momentary depression after evoked release also occurs at intensely stimulated synapses, and suggest that the recovery time may even become shorter under these conditions (although the data come from a different preparation).

6. Momentary silencing and the binomial model. What is n ? What is p ?
Fast recovery from momentary depletion of releasable quanta (or active sites) following evoked release fully explains the lack of correlation in EPP size fluctuations during repetitive stimulation even though the number of active sites (or releasable vesicles) is very limited, as suggested by binomial analysis. Thus, it appears that kinetic and statistical data can be reconciled with a binomial model for quantal release.
Our increasing awareness of the complexity of the synaptic release machinery makes the n × p model for quantal release look as a wildly oversimplified view. However, the binomial model is far more general than it may appear at a first glance. For example, if n vesicle docking sites, competent for evoked release, were present in the presynaptic membrane, and the fusion of a vesicle required the proper location of the vesicle, the correct formation of a multi-molecular protein complex (fusion or SNARE complex) and the opening of one (or more) appropriately located calcium channel(s), then the compound probability of occurrence all of these required conditions (which could be computed, in principle) can be called p, and the system will again be described by binomial statistics with parameters n and p (Figure 8). 



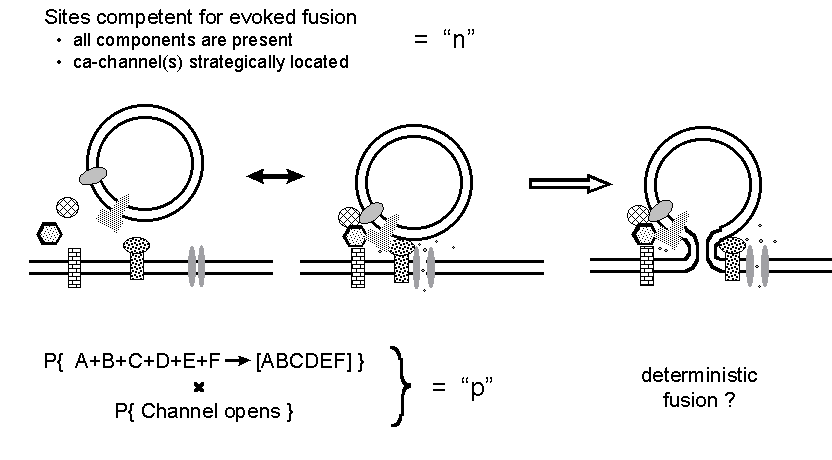
Figure 8. A reinterpretation of the n and p binomial parameters. It is suggested that the stochastic aspects of release concern the assembly of a functional fusion complex and the opening of calcium channel(s) at a competent site, whereas the action potential simply induces exocytosis at all competent sites loaded with an adequately assembled fusion complex. 

The most popular interpretation of the binomial model is based on the idea that in response to the presynaptic spike a defined maximum number (n) of secretory events could occur, each with a fixed probability of occurrence, p. The binomial parameter n is generally thought of as the number of "readily releasable quanta" or, equivalently, sites in a terminal which are ready to release a quantum, i.e. they are loaded with a vesicle which is docked to the presynaptic membrane through an adequately assembled and primed multimolecular fusion complex ("cocked" or docked-competent for fusion); p would then be the probability for each "readily releasable quantum" to be released. Implicit in this interpretation is the idea that the stochastic aspects in quantal release are confined to the last step (release of a releasable quantum) rather than to preceding events (assembly of a releasable quantum). In other words, this view implicitly suggests that the assembly of a vesicle fusion complex competent for evoked release need not be considered as a reversible (stochastic) process, whereas the fusion events is a possible, stochastic consequence of calcium influx during the action potential.
The interpretation proposed in Figure 8 is somewhat reversed: most of the stochastic aspects in this model move here to early steps in the vesicle mobilization and preparation, and the assembly of a "releasable quantum" is more properly considered as an equilibrium (reversible and stochastic) process. The fusion event might add further stochastic variability, but as regards evoked release it might even be a deterministic consequence of calcium inflow during the action potential. Indeed, paired pulse depression at single hippocampal synapses (Stevens and Wang, 1995), as well as random-interval trains and deconvolution data reported above, consistently point not only to transient depression, but to actual silencing of release for a short period (few ms) which follows nerve-evoked secretion. This strongly suggests that whatever can be secreted in response to the action potential is actually released, i.e. the vesicle armed for firing cannot help releasing its content when Ca2+ floods the release site.
It is interesting to examine how such a revised binomial view of the release machinery could explain some intriguing aspects of transmitter release. Let then p represent, according to Figure 8, the combined probability of all elements of the fusion machine correctly assembling and calcium channels opening to let calcium ions in; n would then represent the number of release sites competent for synchronous evoked release, i.e. where all necessary elements are present and a fusion complex can be formed close enough to one or more calcium channels for the action potential to trigger exocytosis. Notice also that the apparent value of n (measured from quantal content variance) would be decreased by heterogeneity of p among the sites.
The parallel changes which are often observed in n and p during stimulation are not easily explained by the traditional interpretation of the binomial model. According to the view here proposed, however, disassembly of protein complexes and partial depletion of vesicles and/or SNARE-complex components would directly produce a decrease in p; some release sites might even be silenced, thereby producing a concomitant decrease in n. Opposite changes would be produced by enhanced fusion-complex formation and/or vesicle mobility.
The dependence of n on extracellular Ca2+ at rest also is puzzling, if n represents the number of readily releasable quanta: in principle, vesicle mobility or the assembly of fusion complexes might be influenced by extracellular Ca2+ concentrations, but there are no indications on how extracellular calcium might influence intracellular organization at rest. The view here proposed, where n represents the number of sites competent for synchronous release in response to an action potential, suggests an alternative interpretation. The organization of the release sites might vary to some extent. In particular, if the number and precise localization of calcium channels recruited by the fusion complex were not fixed, then the number of  sites which can be activated by the action potential (and the heterogeneity of p) would depend on the amount of calcium entering each channel. At low extracellular Ca2+ concentrations, it is very unlikely that a single channel may let in, during an action potential, enough Ca2+ to trigger release; thus, only those sites of release where a sufficient number of Ca2+ channels are favorably located might be capable to release a quantum of transmitter and contribute to n. This would account for the dependence of n on extracellular Ca2+ concentration. During stimulation at low extracellular [Ca2+], as intracellular calcium rises and activation of kinases ensues, mobilization of vesicles and availability of other components might be enhanced, and more sites might be gradually recruited, thereby producing the observed increase in n.
In general, estimates of p do not increase during stimulation as one would expect if vesicle mobility and SNARE complex formation were enhanced by facilitation processes. However, the rate of fusion complex formation might be bounded by limited availability of some of its components (DeBello et al., 1995). An increased probability of asynchronous exocytosis might divert a significant proportion of vesicles along their way to competence for evoked release. Furthermore, studies of responses to paired pulses at single synapses indicate that the onset of facilitation reduces p heterogeneity (Stevens and Wang, 1995). Thus, decreased variability might significantly contribute to the fall (or lack of increase) in estimates of p during repetitive stimulation.

7. Synchronous and  asynchronous release
At difference with evoked release, asynchronous quantal release is only partly dependent on Ca2+, and it can be enhanced by several factors in addition to the facilitation and potentiation processes which also affect evoked release. Hypertonic solutions, black widow spider venom, ouabain  and other drugs induce increased rates of quantal release (see, e.g., Ginsborg and Jenkinson, 1976; Ceccarelli and Hurlbut, 1980), and their actions variably depend on the extracellular concentration of Ca2+ and other divalent ions. Even post-tetanic potentiation affects asynchronous and evoked release to different extents, and can be sustained by divalent cations other than Ca2+ (Hurlbut et al, 1971). It is therefore likely that the synaptic vesicle can follow more than one path to fusion, and that ionic requirements are different along the various paths. Given the high number of interactions which appear to be involved in the formation of a vesicle ready to fire in response to an action potential, it is likely that several intermediate conformations might lead to vesicle fusion in response to local stimuli such as changes in volume and ionic environment. Thus, the concept itself of "readily releasable quanta" might be misleading, as different stimuli might exert specific actions on distinct intermediate complexes. For example, the dissimilar degree of depression of evoked and asynchronous release, observed during sustained stimulation (Figure 2B), suggests that synchronization of release is somehow depressed, or the transition of quanta from a "readily but asynchronously releasable" condition to a "synchronously releasable" condition is somehow impaired. It is very reasonable that a specific conformation might be needed in order for a vesicle fusion complex to be capable of producing instantaneous exocytosis (on the microsecond time scale) in response to a transient increase of local calcium concentration to the 100-mM range (Llinás et al., 1992), and that an increased probability of asynchronous exocytosis might reduce the probability for a vesicle fusion complex to reach such competence for synchronous release.
We have suggested here that the action potential may not act as a stochastic activator of fusion on vesicles which are docked to the presynaptic membrane and primed for fusion, but rather act as a deterministic trigger on fusion complexes competent for synchronous release. If such a population of synchronously releasable quanta - which we may refer to as "armed vesicles" - did exist, then it should be possible to specifically interfere with their formation, i.e. to produce desynchronization of evoked release. Knock-out studies on the proteins of the fusion complex - SNAREs (for review, see Wu and Bellen, 1997) - and observations using clostridial toxins which cleave these same proteins (Montecucco and Schiavo, 1995) yield relevant information on this aspect. Two qualitatively distinct effects are produced on synaptic response by different botulinum toxins that cleave SNAREs on the presynaptic membrane (BoTx A and C) rather than the vesicle SNARE synaptobrevin, (Tetanus toxin and BoTx B; Gansel et al., 1987; Molgo et al., 1989) and these results have been confirmed by knock-out experiments (Broadie et al., 1995). In particular, cleavage or knock-out of synaptobrevin does not abolish asynchronous release and a burst of miniatures can still be elicited by an action potential, but they are not synchronized to give rise to a typical EPSP. Most other treatments and experimental conditions, on the contrary, may even depress more deeply spontaneous as well as evoked release - as it is the case for BoTx A, - but still the few (if any) quanta released by an action potential give rise to a synchronous response. 

CONCLUSIONS
The data here discussed suggest that in interpreting the functional aspects of neurotransmitter release the schema of a pool of readily releasable quanta which, in response to an action potential, have a certain probability of undergoing fusion, may be inadequate. The dynamics of binomial parameters during repetitive stimulation and the demonstration of transient silencing of release during a brief period which follows synchronous transmitter release evoked by the presynaptic action potential point to a different schema (Figure 9) where the vesicle fusion complex assembly is a reversible process and can proceed, at specifically competent sites, to a final state of competence for synchronous release (indicated as armed vesicle in Figure 9). Exocytotic fusion may occur - and be differentially regulated - at several stages in the process, so that several different pools of "readily releasable quanta" may exist, depending on the means used to stimulate release. 

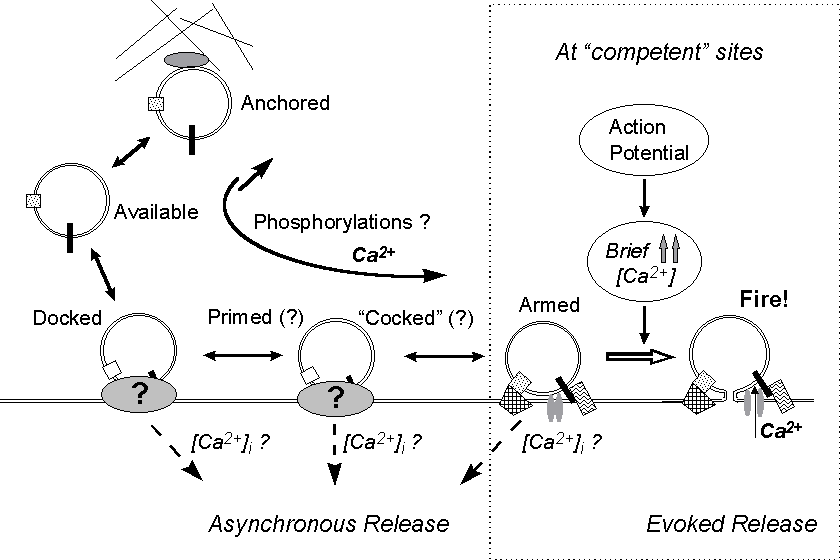
Figure 9. A model for asynchronous and synchronous quantal release. A series of reversible steps lead the vesicle through various conformational stages. Asynchronous release might occur from any of these stages and be differentially regulated by Ca2+ or other factors. Changes in Ca2+ concentration (even in the submicromolar range) and biochemical changes presumably affect the rates and probabilities of the molecular interactions and conformational changes involved. If a fusion complex forms at a release site competent for synchronous evoked fusion - adequately organized and endowed with calcium channel(s) - the vesicle is ready for synchronous release ("armed"); then, if it does not fuse spontaneously before a nerve pulse invades the terminal, it will be discharged in response to the high but rapidly vanishing increase in local Ca2+ level which accompanies the action potential.


This schema suggests that the stochastic nature of quantal release arises from the dynamic equilibrium among the various intermediate forms, whereas the final fusion step following the action potential can be considered as a deterministic, all or none, process, which occurs synchronously, with probability close to 1, at all sites where a competent fusion complex is exposed to a flash of extremely high local calcium concentration, thanks to the proper assembly of a multimolecular complex involving SNARE proteins and calcium channel(s). The model is consistent with the partly common and partly differential sensitivity of spontaneous and evoked release to ionic conditions and experimental situations. In particular, it can account for the sensitivity of both asynchronous and synchronous release to intracellular Ca2+ concentration in the micromolar or submicromolar range, which might sustain facilitation processes by favoring fusion-complex formation. However, the model suggests that only a specific conformation of the fusion complex (armed vesicles) can undergo fusion in response to the huge but rapidly vanishing increase in local Ca2+ concentration that follows the action potential, so that evoked release can be specifically affected by ionic and experimental conditions. This helps interpreting the experimental observations, illustrated by the diagrams in Fig.10, that synchronous quantal release may be preserved, albeit depressed, under conditions which massively inhibit quantal release, but it is selectively impaired by inactivation of specific proteins or by substituting other divalent cations for Ca2+ (e.g. Katz and Miledi, 1967), treatments which presumably interfere with the competence of the fusion complex for synchronous Ca2+-evoked release. 


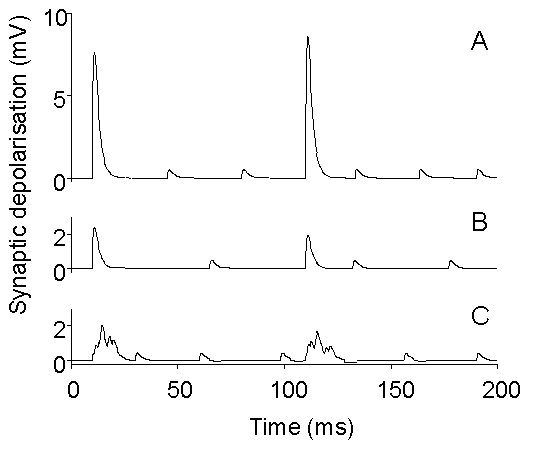
Figure 10. Schematic drawing illustrating the possible differential effects of treatments which inhibit quantal release. A: Simulated evoked and spontaneous EPSPs under control conditions. B: Simulation of overall depression of release, with preserved synchronization of evoked release, as observed, for example, with BoTx A (Gansel et al., 1987) or injection of synthetic SNAP peptides (DeBello et al., 1995). C: Simulation of depression of quantal release with selective disturbance of synchronization, as observed, for example, with tetanus toxin or BoTx B (Gansel et al., 1987) or in synaptotagmin I knock-out mice (Geppert et al., 1994).
 REFERENCES