from: Philosophiocal transactions of the Royal Society
(London)
Biological Sciences, volume 354: pages 319-329, 1999.
[A special issue on "Molecular and cellular aspects of exocytosis]
THE KINETICS OF NERVE-EVOKED
QUANTAL SECRETION
Riccardo Fesce
CNR Center of Cytopharmacology and Dibit,
Dept. Neurosciences, S. Raffaele Scient. Inst.
via Olgettina 58, 20132 Milano - Italy
SUMMARY
Current views on quantal release of neurotransmitters hold that after the
vesicle migrates towards release sites (active zones) multiple protein
interactions mediate the docking of the vesicle to the presynaptic membrane
and the formation of a multimolecular protein complex (the "fusion machine")
which ultimately makes the vesicle competent to release a quantum in response
to the action potential. Classical biophysical studies of quantal release
have modeled the process by a binomial system where n vesicles (sites)
competent for exocytosis release a quantum, with probability p, in response
to the action potential. This is likely to be an oversimplified model;
furthermore, statistical and kinetic studies have given results which are
difficult to reconcile within this framework.
Here, data are presented and discussed which suggest a revision of
the biophysical model. Transient silencing of release is shown to occur
following the pulse of synchronous transmitter release which is evoked
by the presynaptic action potential. This points to a schema where the
vesicle fusion complex assembly is a reversible stochastic process. Asynchronous
exocytosis may occur at several intermediate stages in the process, along
paths which may be differentially regulated by divalent cations or other
factors. The fusion complex becomes competent for synchronous release (armed
vesicles) only at appropriately organized sites. The action potential then
triggers (deterministic-ally rather than stochastically) the synchronous
discharge of all armed vesicles.
The existence of a specific conformation for the fusion complex to
be competent for synchronous evoked fusion reconciles statistical and kinetic
results during repetitive stimulation, and helps explaining the specific
effects of toxins and genetic manipulation on the synchronization of release
in response to an action potential.
INTRODUCTION
It is generally accepted that quantal release of neurotransmitters involves
exocytotic fusion of synaptic vesicles (Ceccarelli and Hurlbut, 1980).
During intense activation of quantal secretion synaptic vesicles undergo
multiple cycles of exo-endocytosis. Although the precise sequence of events
has not been fully clarified, it is generally agreed that vesicles may
be mobilized from a reserve pool - vesicles reversibly associated to the
actin-based cytoskeleton of the nerve terminal through the membrane-associated
phosphoprotein synapsin I - and cluster near specialized sites on the presynaptic
membrane (active zones). Here, the specific interaction among vesicle-membrane
proteins (synaptobrevin, synaptotagmin), soluble factors (N-ethylmaleimide-sensitive
fusion protein or NSF, soluble NSF attachment protein or SNAP, and other
modulatory proteins) and plasmalemmal proteins (syntaxins, synaptosome
associated protein 25 or SNAP-25, calcium channels) promotes the formation
of a multimolecular complex (SNAP receptor protein complex or SNARE complex)
which mediates exocytotic fusion (Calakos and Sheller, 1996; Hanson et
al., 1997). The vesicle membrane may then be retrieved on the spot (Ceccarelli
et al., 1973; Fesce et al., 1994; Palfrey and Artalejo, 1998) or via coated
pits and coated vesicles (Heuser and Reese, 1973; Cremona and De Camilli,
1997).
Morphologically, some vesicles appear in close contact with the presynaptic
membrane at the active zones ("docked" vesicles). However, the precise
molecular features of vesicle docking are not clear. Attempts have been
performed at defining whether each protein involved in exocytosis comes
into play before or after docking, and vesicles ready for exocytosis have
sometimes been indicated as "cocked" - or docked and competent for release.
The term "readily releasable quanta" has also been used in the literature;
this implicitly suggests that vesicles appropriately positioned and primed
by protein interactions might undergo spontaneous exocytosis and also display
a defined probability of releasing their quantum in response to the action
potential.
Actually, no precise functional meaning can be attributed to any of
these terms. In particular, competence for fusion has been evaluated
using several different means of stimulation - hypertonic solutions, elevated
K+, toxins, drugs or electrical stimulation - although no evidence is available
to indicate that the various treatments act on the same vesicle conformation(s)
and population(s).
Here we shall discuss how the concurrent analysis of asynchronous quantal
release and synchronous release evoked by the presynaptic action potential
might help in dissecting functionally defined stages in the exocytotic
cycle, based on the statistical and kinetic properties of the secretory
activity.
1. Approaches to statistical and kinetic analysis of
quantal release
The history of electrophysiology of quantal release is half a century
long. During these decades, the initial hope that the mechanisms of transmitter
release and the properties of the synaptic secretory machinery might be
clarified and understood by means of quantitative statistical and kinetic
analysis of postsynaptic responses has gradually surrendered to the ever
growing awareness of the complexity of transmitter release modulation by
a multitude of functional, biochemical and pharmacological factors.
A classical approach to the study of quantal release has been the statistical
analysis of fluctuations in quantal content of synaptic responses evoked
by presynaptic stimulation at low frequency. The statistics of quantal
content in successive responses to electrical stimulation can be described
by binomial statistics at many synapses, and this has suggested that a
defined number n of entities (be they releasable vesicles, release
sites or active zones) can produce the release of a quantum of transmitter,
with probability p, in response to a presynaptic stimulus. However,
estimated values and changes of n and p under various experimental conditions
could not be easily reconciled with a comprehensive and consistent interpretation.
Most difficulties in this approach presumably arise from the unreliability
of the estimated binomial parameters, in the presence of heterogeneous
probability of release and temporal variability during repetitive stimulation,
which cannot be spotted by standard binomial analysis but markedly affect
the estimates (see Brown et al. 1976). Although these problems might in
principle be overcome by more sophisticated approaches to statistical analysis
of quantal content (Courtney, 1978; Miyamoto, 1986; Fesce, 1990),
this path has not been systematically explored.
A conceptually different, kinetic approach was also employed in investigating
the question: the probability of release was estimated from the decrease
in endplate potential (EPP) amplitude (or in quantal content) in response
to pairs or trains of stimuli delivered at short intervals (Liley and North,
1953, Thies, 1965; Elmqvist and Quastel, 1965). Mallart and Martin
(1967) combined the regression of quantal content on total past release
with ensemble averaging over several trains of stimuli, to reduce fluctuations
and increase the reliability of the approach. In the absence of recycling
(i.e. at sufficiently short intervals between successive stimuli) the fractional
decrease in quantal content between the stimuli should reflect the fraction
of available quanta released (or release sites activated) by the first
stimulus - i.e. p - and the regression of quantal content (m
= n × p) on total past release (which should parallel
the decrease in n, in the absence of recycling) should also yield
an estimate of p. Although this approach seemed self-evident, a
series of undemonstrated (or even false) assumptions were implicit in it:
even accepting that n entities with probability p of determining
release of a quantum are sufficient to describe the system and no recycling
occurs in short time intervals, no evidence indicates that p will
remain unaltered between successive stimuli. Indeed, Betz (1970) and Christensen
& Martin (1970) demonstrated that the decrease in quantal content of
the second EPP is not linearly but rather quadratically related to the
size of the first EPP, thereby suggesting that p is decreased to about
the same extent as n, as a consequence of release in response to
the first stimulus; the authors proposed that preferential release of high-probability
quanta in response to the first stimulus might explain this finding. However,
it appears that this approach also is unable to yield clear-cut and
consistent answers to the question of what statistical and kinetic parameters
determine the quantal content of evoked responses.
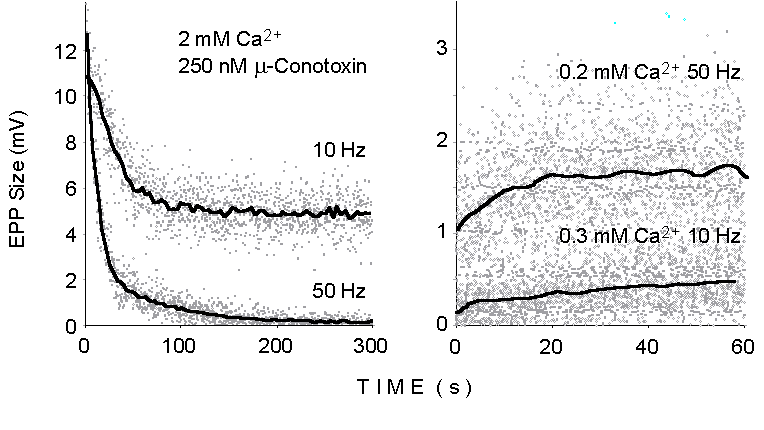
Figure 1. The dots illustrate the peak
size of successive EPPs recorded at motor endplates in the mouse extensor
digitorum longus (EDL) muscle during trains of stimuli delivered to the
sciatic nerve at various stimulation frequencies and under the different
experimental conditions indicated. The lines display momentary average
values smoothed over time. 250 nM mu-Conotoxin added at normal Ca2+
concentration (2 mM; left panel) to prevent muscle action potential and
twitching.
2. Binomial analysis during sustained electrical stimulation
At the neuromuscular junction, markedly heterogeneous time courses
can be induced in EPP size and quantal content by repetitive stimulation
at relatively high frequency (10-100 Hz). Figure 1 illustrates the declining
responses observed during repetitive stimulation at 10 and 50 Hz in physiological
extracellular Ca2+ concentration (Left: 2 mM Ca2+,
250 nM mu-Conotoxin added to prevent muscle action potential) and the growing
responses at lowered Ca2+ concentrations (Right: 10 Hz, 0.3
mM Ca2+; 50 Hz, 0.2 mM Ca2+). Such changes reflect
the dynamic balance between synaptic facilitation and potentiation processes
on the one hand and synaptic depression or vesicle depletion on the other.
Spontaneous quantal release can be measured by counting the mEPPs which
occur between pairs of successive stimuli: during repetitive stimulation
asynchronous release is also affected by facilitation and depression processes.
However, asynchronous and evoked quantal release are known to be differentially
regulated by Ca2+ and other divalent ions and dissimilarly affected
by drugs and toxins. Figure 2 shows that also repetitive stimulation produces
differential effects on evoked and asynchronous release: initial facilitation
phenomena are markedly more evident in mEPP rate than in EPP size, whereas
profound depression of evoked, but not asynchronous, release is apparent
at late times during high-frequency stimulation in normal Ca2+.
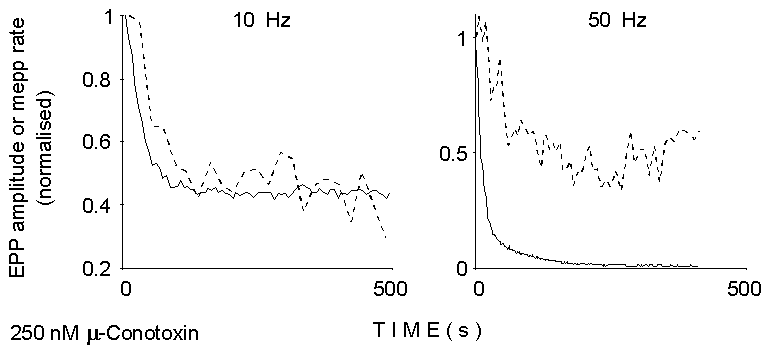 0
0
Figure 2. Smoothed time courses of EPP
size and mEPP rate of occurrence between EPPs during the two trains of
stimuli illustrated in Figure 1 (left). Calcium concentration, 2 mM; 250
nM mu-Conotoxin. Notice the delay in depression of asynchronous release
at 10 Hz, and the initial facilitation and less prominent depression at
50 Hz.
The results of binomial analysis under these experimental conditions
are illustrated in Figure 3. The results are consistent with a binomial
model, as they point to a limited value for the parameter n, in
agreement with most previously published observations under various experimental
conditions. The decrease of the n parameter during the train in
normal calcium is not unexpected and may reflect quantal depletion and/or
fatigue; instead, the apparent increase in n, rather than p,
in low Ca2+, is puzzling, as is the decrease in p which
is observed in normal Ca2+ (although previous similar analyses
also suggested a concurrent decline in both n and p during repetitive stimulation
which produces synaptic depression; Mallart and Martin, 1967).
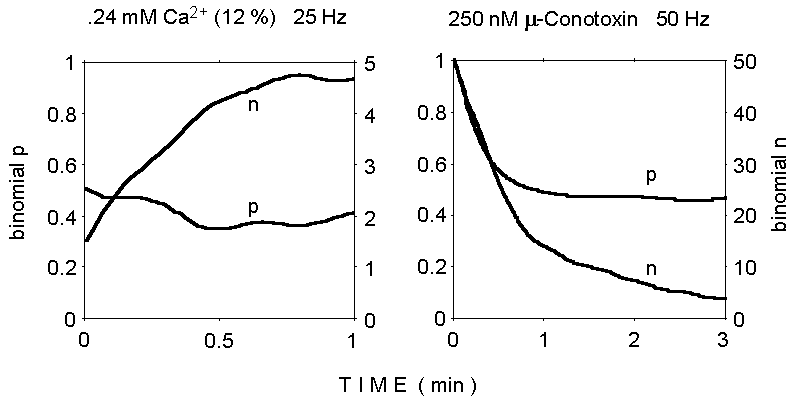
Figure 3. Binomial analysis of quantal
content of EPPs during two trains of stimuli. Notice the gradual increase
of binomial n from the initial very low value at reduced Ca2+
concentration (left panel), and the decrease in both n and p during stimulation
at 50 Hz in normal Ca2+ concentration (2 mM; 250 nM mu-Conotoxin
added; right panel).
The main problems arising with binomial analysis are related to variability
among the p values for different sites - which decreases response
variance - and to variability of n and p in time - which
increase response variance. Although such phenomena prevent accurate and
meaningful estimates of the parameters, relative changes in the estimates
during an experiment or under different experimental conditions still yield
relevant information on the underlying processes.
3. Correlation analysis
Under all conditions here examined the estimates of n at late
times are consistently very low (< 10). It is worth pointing out that,
although estimates of n and p may be inadequate, quantal
analysis yields a solid piece of information: the variance in quantal content
is too low for a Poisson system (characterized by a high number of possible
events occurring with very low probability). Such low variance obviously
is an important positive feature in terms of information processing at
the synapse, and it might be observed that both a limited number of functional
release sites and heterogeneous probabilities of release are advantageous
features in terms of decreased output variability.
The clear indication of a limited number of release sites was exploited
in the past to try and get relevant information on the process from the
analysis of successive responses in a train of high frequency stimuli.
A more robust approach would be the application of autoregressive analysis
to quantal contents during sustained stimulation. In particular, one could
investigate the autocorrelation of EPP sizes (or quantal contents) in a
reasonably stationary condition, i.e. the dependence of the size of each
EPP on the size of the previous one, during prolonged stimulation. EPPs
with a particularly high quantal content (due to random fluctuation) should
be preferentially followed by undersized EPPs (due to larger momentary
depletion). Systematic analyses by this approach should be able to validate
the n × p model while yielding information on both
parameters and on the time constant of the quantum reconstitution process.
A problem arises if the parameters of the secretory process change
with time. In this case, oversized and undersized EPPs will tend to cluster
(positive correlation of EPP sizes), reflecting changes in momentary mean
values. This idea was used to investigate whether slow fluctuations in
transmitter release are sustained by calcium fluctuations in the nerve
terminal (Meiri and Rahamimoff, 1978). However, even though the mean EPP
size may change with time, the departures of EPP sizes from the momentary
mean value need not be correlated, unless the quantal content of an EPP
directly influences subsequent output .
If an almost steady state can be reached, the number of quanta recovered
between stimuli will balance the expected number of quanta lost (n
× p). Whenever an EPP with quantal content greater than expected
occurs (m > n × p) the number of quanta available
for next EPP should decrease by the number of quanta released in excess
(e) and quantal content should be transiently depressed (by a factor
close to e × p, neglecting rapid recycling). Such an
effect of random fluctuations of quantal content on subsequent responses
should be detectable if n is small (and thereby significantly affected
by small changes in quantal release) and should fade away with the time
constant of quantum reconstitution. In other words, the autocorrelation
of the departures of quantal content from its momentary mean value should
pinpoint the memory of the system.
More precisely, let nj be the number of activatable
sites at stimulus j, and pj the corresponding
probability of release. The expected quantal content is E[mj]
= nj × pj. For a constant p
and in the absence of recycling, we would have nj+1 =
n0 - SUM[m0, m1,
m2 ... mj], and E[mj+1]
= (n0 - SUM[m0, m1,
m2 ... mj]) × p. Thus,
-p would be the slope of quantal content versus cumulative previous
release (Elmqvist and Quastel, 1965). If rj quanta
are refilled between stimuli j and j+1, the available sites
at stimulus j+1 will be nj+1 = nj
- mj + rj . Thus, the next expected
quantal content will be E[mj+1] = (nj
- mj + rj) × pj+1.
If the stimulation proceeds until a steady state is reached, p will
become constant and the average values of m (<m>) and
of r (<r>) should become equal (release equals refilling).
Thus, at steady state, E[mj +1 - m] = (nj - mj + rj) ×
p - m = E[mj - m] - (mj - rj) × p
and E[(mj+1 - <m>) - (1 - p)
× (mj - <m>)] = (rj
- <r>) × p.
If the departures of r from its mean value are random, this
equation defines a first order autoregressive system, so that simple mathematical
processing of the autocorrelation of fluctuations in quantal content at
steady state should yield a value for p. In particular, the autocorrelation
of quantal content should display the behavior illustrated in Figure 4A.
However, if the recycling/refilling speed were highly correlated with quantal
content (i.e. most of the quanta released in response to a stimulus are
rapidly reconstituted before next stimulus), then no correlation should
be detectable.
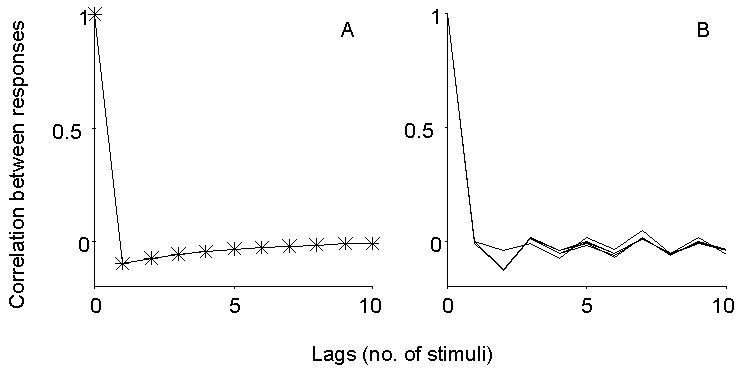
Figure 4. Expected and observed autocorrelation
of EPP size fluctuations during repetitive stimulation. Left panel illustrates
the expected behavior for low n and transient depression following oversized
EPPs (see text). The right panel shows the autocorrelation computed at
late times during trains of stimuli at 10 and 50 Hz in 2 mM Ca2+
and 250 nM mu-Conotoxin, at 25 and 50 Hz in 0.3 mM Ca2+ (15%)
and at 100 Hz in 0.24 mM Ca2+ (12%). No consistent autocorrelation
is observed on the fast time scale here considered, and in particular no
undershoot is observed for lag=1, as would instead be expected for a small
pool of quanta subject to momentary depletion.
Actually, one may ask why such an approach has not been previously
applied at all. The answer is probably a simple one: negative results never
get published. In fact, no dependence of EPP quantal content on the size
of previous EPPs could be detected at the mouse EDL muscle during repetitive
stimulation, at frequencies from 10 to 100 Hz and under conditions of depressed
as well as normal quantal content. Figure 4B illustrates the autocorrelation
of EPP sizes at steady state during trains of stimuli in normal Ca2+
(250 nM mu-Conotoxin) at 10 or 50 Hz, and in reduced Ca2+ concentration
(0.3 mM, 25 or 50 Hz; 0.24 mM, 100 Hz). No significant correlation could
be detected under any of these conditions, although inconsistent fluctuations
on a longer time scale were often apparent.
If momentary depletion occurred after each stimulus, and its extent
were related to recent quantal output, negative correlation should arise
between EPP size and mEPP frequency between successive stimuli. Again,
as shown in Figure 5, no significant autocorrelation could be detected
for either EPPs or mEPPs and no cross-correlation was apparent between
EPPs and mEPPs. These results are difficult to reconcile with a binomial
model, considering in particular that estimates of n at steady state are
quite small (< 10) for the repetitive stimulation protocols examined
here.
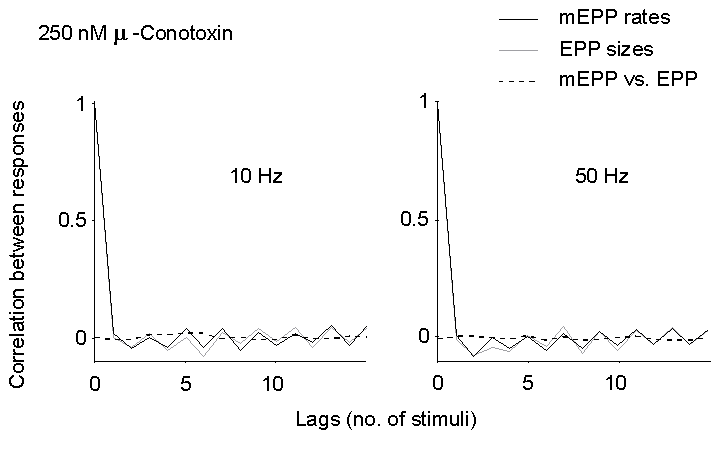
Figure 5. Autocorrelation of EPP size and
mEPP rate of occurrence (between EPPs), and cross-correlation of mEPP rate
vs. EPP size at late times during trains of stimuli in 2 mM Ca2+
and 250 nM mu-Conotoxin. No significant correlation can be detected, either
at 10 or 50 Hz.
4. Is a binomial model (and a statistical model in
general) of any usefulness ?
Even though statistical and kinetic analysis of quantal content are
unable to yield a consistent dynamic model of the release machinery, the
conceptual framework of binomial statistics is helpful in considering the
features of information processing at the synapse. An optimally designed
synapse, in terms of consistency of information processing, should display
both low variability under stationary conditions and no memory of past
output (and especially of its random fluctuations) under repetitive stimulation.
If one were to choose a statistical system for quantal release such that
error (and variability) is kept to a minimum, a limited number of release
sites with high probability of releasing a quantum would fit best, and
quantal contents would obey binomial statistics with finite n, as
observed distributions at rest usually do; on the other hand, such a system
would be affected by correlation between successive events (occasional
oversized responses would significantly depress subsequent release) whereas
an unlimited number of release sites with very low release probability
(a Poisson system) would be best to grant the observed independence.
Thus, simple models may be inadequate to describe the synaptic release
machinery, which is endowed with a particularly favorable behavior: it
is characterized by low variability (high reliability) under basal conditions;
it can be modulated by activity over a wide range of efficiency levels;
still, it is sufficiently memoriless not to be affected by random fluctuations
in its own previous output (low correlation and again high reliability).
An intriguing perspective which has not been investigated in detail
regards the possibility that release may actually produce a momentary depression
of activated release sites, but refilling of the active sites (or of a
readily releasable pool of vesicles) might be so fast that the momentary
depletion which follows a release event is rapidly recovered from before
the next stimulus arrives, and no correlation between successive responses
can be observed.
5. Recovery between stimuli
Alternative hypotheses can be put forward to explain the lack of correlation
between successive EPPs at steady state: release sites might be loaded
with more than one releasable quantum although they release only one at
a time; the number of quanta and/or release sites might be so high that
the number of quanta released with any single EPP cannot noticeably affect
the release machinery (although this is in contradiction with the low values
for n consistently reported in the literature).
In order to investigate these possibilities neuromuscular junctions
were subjected to "random interval" stimulation, i.e. repetitive stimulation
at variable time intervals, with mean stimulation rates of 10-20 Hz. The
analysis of a representative experiment is illustrated in Figure 6. Here,
the average interval between stimuli was 67 ms (15 Hz) and extracellular
Ca2+ concentration was 0.4 mM. The average EPP sizes (groups
of 166 successive EPPs) are plotted on the left as a function of time,
to illustrate the overall time course of release. On the right, the departures
of EPP sizes from the momentary average were computed and the values were
grouped according to the time interval between the corresponding stimulus
and the previous one. The decaying facilitation is apparent from the smooth
curve (two-exponential decay with time constants about 10 and 70 ms).
However, at short time intervals the data depart from the exponential decay
fit to the data, suggesting an initial depression which fades away with
a time constant of about 6 ms.
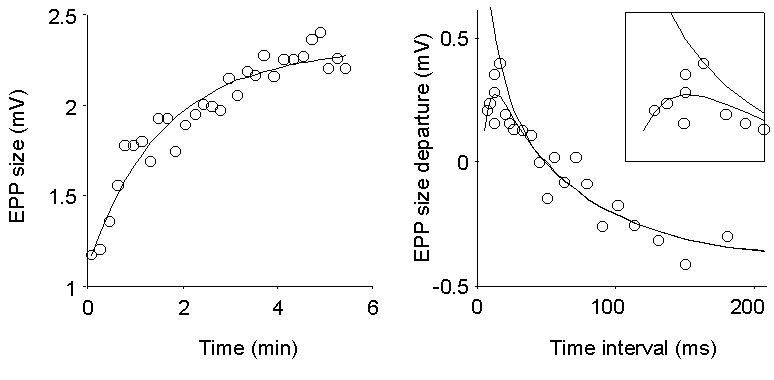
Figure 6. Analysis of EPP sizes during
stimulation at random time intervals. Mean stimulation frequency, 15 Hz;
0.4 mM Ca2+ (20%). Left panel shows successive averages
of groups of 166 EPPs and a smooth analytical fit to the overall time course
(two-exponential rise with time constants of 75 and 175 s, respectively).
Right panel displays the departures of EPP sizes from the momentary average;
each point represents 100 EPPs, grouped according to the time interval
which precedes the corresponding stimulus. The smooth decaying indicates
facilitation which decreases as the interval gets longer. It is well fit
by a two-exponential decay with time constants of 68 and 9.8 ms, respectively.
For short intervals, the points fall below the fit, indicating an initial
depression, which vanishes with a 6.5 ms time constant (see also inset).
This suggests that a momentary depletion of releasable quanta (or silencing
of release sites) does occur after each episode of evoked release, although
recovery is so rapid (within 10-20 ms) that no "memory" of recent output
is detected for stimulation rates up to 50 Hz.
In order to further investigate this point, an autoregressive deconvolution
procedure (Fesce, 1990; Sacchi et al., 1998) was applied to the time course
of the averaged EPPs during repetitive stimulation. Figure 7 illustrates
the results of this approach for a train of stimuli at 50 Hz in normal
extracellular Ca2+ concentration: the average EPP time courses are shown
for the first 150 EPPs in the train and for groups of 1000 EPPs at 2 and
5 min after the onset of stimulation (upper left). The analytical shape
of the mEPPs (the difference between two exponentials, fit to averaged
mEPPs isolated from the same recording) was deconvolved into the average
EPP waveform to yield an estimate of the probability of release as a function
of time after the delivery of the stimulus (upper right). Deconvolution
reveals a peaky pulse of synchronous release (for the initial oversized
EPPs nonlinear summation is relevant and somewhat smoothens the peak, giving
rise to an artifactual shoulder on the decay phase). The pulse of synchronous
release is delayed at late times, but is over by 2 ms after the stimulus,
and is followed by a tiny tail of release. The relative relevance of the
tail is appreciated from the cumulative release curves (lower left) which
are obtained by integrating the probability of release over time. The tail
becomes more prominent at late times, in agreement with the less marked
depression observed for asynchronous release (Figure 2). The cumulative
release curves display a momentary flattening (particularly apparent for
late EPPs) which precedes the slow asymptotically rising phase. This indicates
temporary silencing of release. Inspection of the curves of release probability
at high amplification (lower right) confirms this impression: the probability
of release decays exponentially at times greater than 5 ms, but backward
extrapolation of the decay highlights the temporary silencing that follows
synchronous release, from which the synapse rapidly recovers.
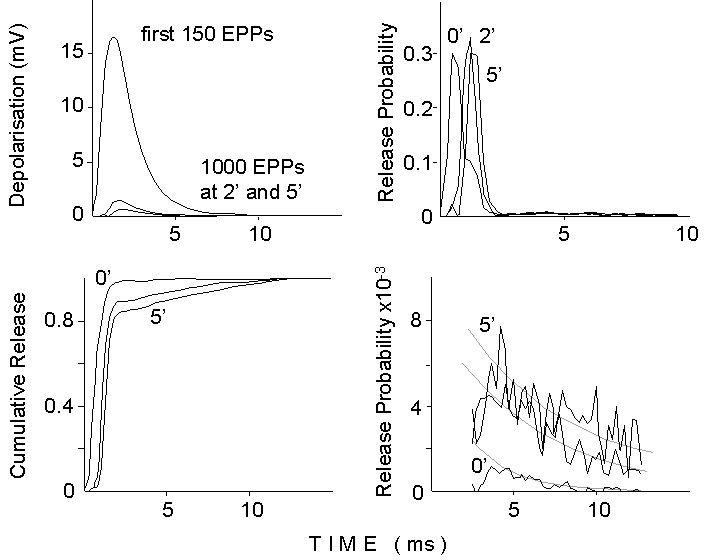
Figure 7. Deconvolution analysis of the
EPP waveform during a 50 Hz train of stimuli delivered in 2 mM Ca2+
and 250 nM mu-Conotoxin. Top left: average waveform for the first 150 EPPs
and for groups of 1000 EPPs at 2 and 5 minutes after the onset of the stimulation.
Top right: Release probability curves obtained by deconvolving the average
mEPP waveform (the difference between two exponentials with 0.6 ms rise
time constant and 4 ms decay time constant) into the averaged EPP. Notice
the shoulder in the deconvolution for the first group (0 min), produced
by flattening of the peak, due to nonlinear summation, for the first oversized
EPPs. Bottom left: cumulative release curves obtained by integrating the
release probability curves. Notice momentary flattening and increasing
slow component for later times. Bottom right: tails of release probability
curves redisplayed at higher gain (the first 3 ms have been canceled).
Notice the initial depression and the exponential decays, after 4-5 ms.
The results of random-interval stimulation and deconvolution of the
EPP waveform indicate that temporary silencing of release follows synchronous
secretion induced by the action potential during sustained stimulation.
Paired pulse experiments at single hippocampal synapses at rest (Stevens
and Wang, 1995) revealed a rapidly waning depression (about 5 ms silencing
followed by recovery with a time constant of about 5 ms) at synapses where
a quantum had just been released. From those experiments it could not be
concluded whether such a depression would also be present (and if so, to
what extent) at actively secreting synapses. The data here recalled indicate
that momentary depression after evoked release also occurs at intensely
stimulated synapses, and suggest that the recovery time may even become
shorter under these conditions (although the data come from a different
preparation).
6. Momentary silencing and the binomial model. What
is n ? What is p ?
Fast recovery from momentary depletion of releasable quanta (or active
sites) following evoked release fully explains the lack of correlation
in EPP size fluctuations during repetitive stimulation even though the
number of active sites (or releasable vesicles) is very limited, as suggested
by binomial analysis. Thus, it appears that kinetic and statistical data
can be reconciled with a binomial model for quantal release.
Our increasing awareness of the complexity of the synaptic release
machinery makes the n × p model for quantal release look as
a wildly oversimplified view. However, the binomial model is far more general
than it may appear at a first glance. For example, if n vesicle
docking sites, competent for evoked release, were present in the presynaptic
membrane, and the fusion of a vesicle required the proper location of the
vesicle, the correct formation of a multi-molecular protein complex (fusion
or SNARE complex) and the opening of one (or more) appropriately located
calcium channel(s), then the compound probability of occurrence all of
these required conditions (which could be computed, in principle) can be
called p, and the system will again be described by binomial statistics
with parameters n and p (Figure 8).
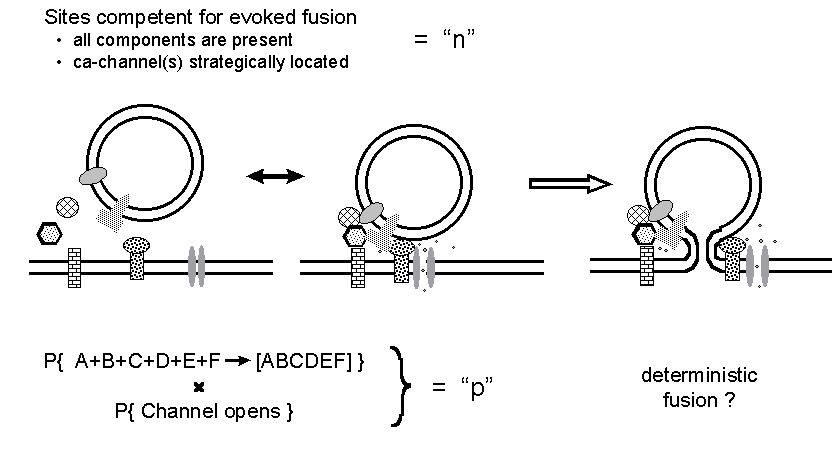
Figure 8. A reinterpretation of the n and
p binomial parameters. It is suggested that the stochastic aspects of release
concern the assembly of a functional fusion complex and the opening of
calcium channel(s) at a competent site, whereas the action potential simply
induces exocytosis at all competent sites loaded with an adequately assembled
fusion complex.
The most popular interpretation of the binomial model is based on the
idea that in response to the presynaptic spike a defined maximum number
(n) of secretory events could occur, each with a fixed probability
of occurrence, p. The binomial parameter n is generally thought
of as the number of "readily releasable quanta" or, equivalently, sites
in a terminal which are ready to release a quantum, i.e. they are loaded
with a vesicle which is docked to the presynaptic membrane through an adequately
assembled and primed multimolecular fusion complex ("cocked" or docked-competent
for fusion); p would then be the probability for each "readily releasable
quantum" to be released. Implicit in this interpretation is the idea that
the stochastic aspects in quantal release are confined to the last step
(release of a releasable quantum) rather than to preceding events (assembly
of a releasable quantum). In other words, this view implicitly suggests
that the assembly of a vesicle fusion complex competent for evoked release
need not be considered as a reversible (stochastic) process, whereas the
fusion events is a possible, stochastic consequence of calcium influx during
the action potential.
The interpretation proposed in Figure 8 is somewhat reversed: most
of the stochastic aspects in this model move here to early steps in the
vesicle mobilization and preparation, and the assembly of a "releasable
quantum" is more properly considered as an equilibrium (reversible and
stochastic) process. The fusion event might add further stochastic variability,
but as regards evoked release it might even be a deterministic consequence
of calcium inflow during the action potential. Indeed, paired pulse depression
at single hippocampal synapses (Stevens and Wang, 1995), as well as random-interval
trains and deconvolution data reported above, consistently point not only
to transient depression, but to actual silencing of release for a short
period (few ms) which follows nerve-evoked secretion. This strongly suggests
that whatever can be secreted in response to the action potential is actually
released, i.e. the vesicle armed for firing cannot help releasing its content
when Ca2+ floods the release site.
It is interesting to examine how such a revised binomial view of the
release machinery could explain some intriguing aspects of transmitter
release. Let then p represent, according to Figure 8, the combined
probability of all elements of the fusion machine correctly assembling
and calcium channels opening to let calcium ions in; n would then
represent the number of release sites competent for synchronous evoked
release, i.e. where all necessary elements are present and a fusion complex
can be formed close enough to one or more calcium channels for the action
potential to trigger exocytosis. Notice also that the apparent value of
n (measured from quantal content variance) would be decreased by
heterogeneity of p among the sites.
The parallel changes which are often observed in n and p
during stimulation are not easily explained by the traditional interpretation
of the binomial model. According to the view here proposed, however, disassembly
of protein complexes and partial depletion of vesicles and/or SNARE-complex
components would directly produce a decrease in p; some release
sites might even be silenced, thereby producing a concomitant decrease
in n. Opposite changes would be produced by enhanced fusion-complex
formation and/or vesicle mobility.
The dependence of n on extracellular Ca2+ at rest
also is puzzling, if n represents the number of readily releasable
quanta: in principle, vesicle mobility or the assembly of fusion complexes
might be influenced by extracellular Ca2+ concentrations, but
there are no indications on how extracellular calcium might influence intracellular
organization at rest. The view here proposed, where n represents the number
of sites competent for synchronous release in response to an action potential,
suggests an alternative interpretation. The organization of the release
sites might vary to some extent. In particular, if the number and precise
localization of calcium channels recruited by the fusion complex were not
fixed, then the number of sites which can be activated by the action
potential (and the heterogeneity of p) would depend on the amount
of calcium entering each channel. At low extracellular Ca2+
concentrations, it is very unlikely that a single channel may let in, during
an action potential, enough Ca2+ to trigger release; thus, only
those sites of release where a sufficient number of Ca2+ channels
are favorably located might be capable to release a quantum of transmitter
and contribute to n. This would account for the dependence of n
on extracellular Ca2+ concentration. During stimulation at low
extracellular [Ca2+], as intracellular calcium rises and activation
of kinases ensues, mobilization of vesicles and availability of other components
might be enhanced, and more sites might be gradually recruited, thereby
producing the observed increase in n.
In general, estimates of p do not increase during stimulation
as one would expect if vesicle mobility and SNARE complex formation were
enhanced by facilitation processes. However, the rate of fusion complex
formation might be bounded by limited availability of some of its components
(DeBello et al., 1995). An increased probability of asynchronous exocytosis
might divert a significant proportion of vesicles along their way to competence
for evoked release. Furthermore, studies of responses to paired pulses
at single synapses indicate that the onset of facilitation reduces p heterogeneity
(Stevens and Wang, 1995). Thus, decreased variability might significantly
contribute to the fall (or lack of increase) in estimates of p during repetitive
stimulation.
7. Synchronous and asynchronous release
At difference with evoked release, asynchronous quantal release is
only partly dependent on Ca2+, and it can be enhanced by several
factors in addition to the facilitation and potentiation processes which
also affect evoked release. Hypertonic solutions, black widow spider venom,
ouabain and other drugs induce increased rates of quantal release
(see, e.g., Ginsborg and Jenkinson, 1976; Ceccarelli and Hurlbut, 1980),
and their actions variably depend on the extracellular concentration of
Ca2+ and other divalent ions. Even post-tetanic potentiation
affects asynchronous and evoked release to different extents, and can be
sustained by divalent cations other than Ca2+ (Hurlbut et al,
1971). It is therefore likely that the synaptic vesicle can follow more
than one path to fusion, and that ionic requirements are different along
the various paths. Given the high number of interactions which appear to
be involved in the formation of a vesicle ready to fire in response to
an action potential, it is likely that several intermediate conformations
might lead to vesicle fusion in response to local stimuli such as changes
in volume and ionic environment. Thus, the concept itself of "readily releasable
quanta" might be misleading, as different stimuli might exert specific
actions on distinct intermediate complexes. For example, the dissimilar
degree of depression of evoked and asynchronous release, observed during
sustained stimulation (Figure 2B), suggests that synchronization of release
is somehow depressed, or the transition of quanta from a "readily but asynchronously
releasable" condition to a "synchronously releasable" condition is somehow
impaired. It is very reasonable that a specific conformation might be needed
in order for a vesicle fusion complex to be capable of producing instantaneous
exocytosis (on the microsecond time scale) in response to a transient increase
of local calcium concentration to the 100-mM range (Llinás et al.,
1992), and that an increased probability of asynchronous exocytosis might
reduce the probability for a vesicle fusion complex to reach such competence
for synchronous release.
We have suggested here that the action potential may not act as a stochastic
activator of fusion on vesicles which are docked to the presynaptic membrane
and primed for fusion, but rather act as a deterministic trigger on fusion
complexes competent for synchronous release. If such a population of synchronously
releasable quanta - which we may refer to as "armed vesicles" - did exist,
then it should be possible to specifically interfere with their formation,
i.e. to produce desynchronization of evoked release. Knock-out studies
on the proteins of the fusion complex - SNAREs (for review, see Wu and
Bellen, 1997) - and observations using clostridial toxins which cleave
these same proteins (Montecucco and Schiavo, 1995) yield relevant information
on this aspect. Two qualitatively distinct effects are produced on synaptic
response by different botulinum toxins that cleave SNAREs on the presynaptic
membrane (BoTx A and C) rather than the vesicle SNARE synaptobrevin, (Tetanus
toxin and BoTx B; Gansel et al., 1987; Molgo et al., 1989) and these results
have been confirmed by knock-out experiments (Broadie et al., 1995). In
particular, cleavage or knock-out of synaptobrevin does not abolish asynchronous
release and a burst of miniatures can still be elicited by an action potential,
but they are not synchronized to give rise to a typical EPSP. Most other
treatments and experimental conditions, on the contrary, may even depress
more deeply spontaneous as well as evoked release - as it is the case for
BoTx A, - but still the few (if any) quanta released by an action potential
give rise to a synchronous response.
CONCLUSIONS
The data here discussed suggest that in interpreting the functional aspects
of neurotransmitter release the schema of a pool of readily releasable
quanta which, in response to an action potential, have a certain probability
of undergoing fusion, may be inadequate. The dynamics of binomial parameters
during repetitive stimulation and the demonstration of transient silencing
of release during a brief period which follows synchronous transmitter
release evoked by the presynaptic action potential point to a different
schema (Figure 9) where the vesicle fusion complex assembly is a reversible
process and can proceed, at specifically competent sites, to a final state
of competence for synchronous release (indicated as armed vesicle in Figure
9). Exocytotic fusion may occur - and be differentially regulated - at
several stages in the process, so that several different pools of "readily
releasable quanta" may exist, depending on the means used to stimulate
release.
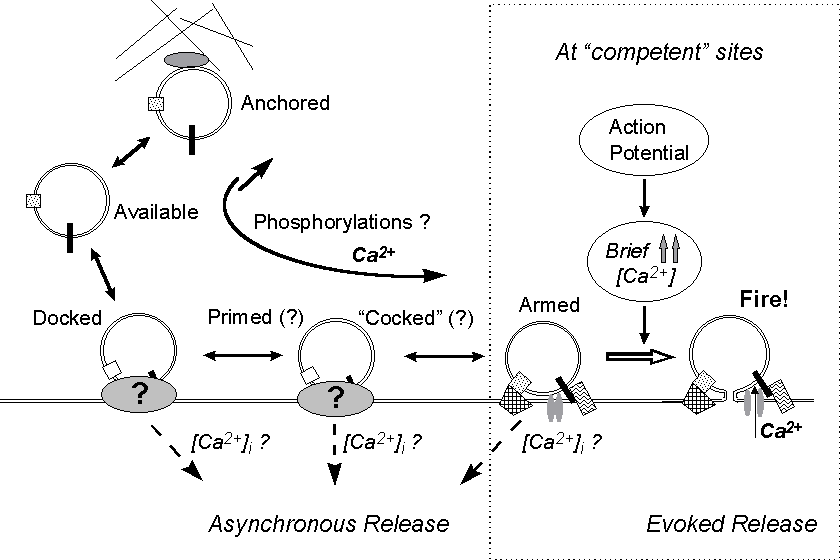
Figure 9. A model for asynchronous and synchronous
quantal release. A series of reversible steps lead the vesicle through
various conformational stages. Asynchronous release might occur from any
of these stages and be differentially regulated by Ca2+ or other factors.
Changes in Ca2+ concentration (even in the submicromolar range) and biochemical
changes presumably affect the rates and probabilities of the molecular
interactions and conformational changes involved. If a fusion complex forms
at a release site competent for synchronous evoked fusion - adequately
organized and endowed with calcium channel(s) - the vesicle is ready for
synchronous release ("armed"); then, if it does not fuse spontaneously
before a nerve pulse invades the terminal, it will be discharged in response
to the high but rapidly vanishing increase in local Ca2+ level which accompanies
the action potential.
This schema suggests that the stochastic nature of quantal release
arises from the dynamic equilibrium among the various intermediate forms,
whereas the final fusion step following the action potential can be considered
as a deterministic, all or none, process, which occurs synchronously, with
probability close to 1, at all sites where a competent fusion complex is
exposed to a flash of extremely high local calcium concentration, thanks
to the proper assembly of a multimolecular complex involving SNARE proteins
and calcium channel(s). The model is consistent with the partly common
and partly differential sensitivity of spontaneous and evoked release to
ionic conditions and experimental situations. In particular, it can account
for the sensitivity of both asynchronous and synchronous release to intracellular
Ca2+ concentration in the micromolar or submicromolar range,
which might sustain facilitation processes by favoring fusion-complex formation.
However, the model suggests that only a specific conformation of the fusion
complex (armed vesicles) can undergo fusion in response to the huge but
rapidly vanishing increase in local Ca2+ concentration that
follows the action potential, so that evoked release can be specifically
affected by ionic and experimental conditions. This helps interpreting
the experimental observations, illustrated by the diagrams in Fig.10, that
synchronous quantal release may be preserved, albeit depressed, under conditions
which massively inhibit quantal release, but it is selectively impaired
by inactivation of specific proteins or by substituting other divalent
cations for Ca2+ (e.g. Katz and Miledi, 1967), treatments which
presumably interfere with the competence of the fusion complex for synchronous
Ca2+-evoked release.
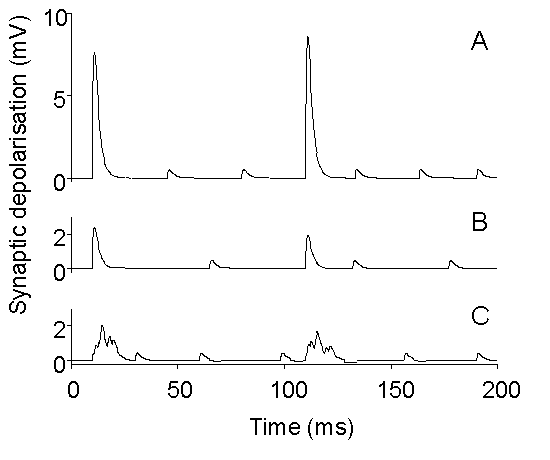
Figure 10. Schematic drawing illustrating
the possible differential effects of treatments which inhibit quantal release.
A: Simulated evoked and spontaneous EPSPs under control conditions. B:
Simulation of overall depression of release, with preserved synchronization
of evoked release, as observed, for example, with BoTx A (Gansel et al.,
1987) or injection of synthetic SNAP peptides (DeBello et al., 1995). C:
Simulation of depression of quantal release with selective disturbance
of synchronization, as observed, for example, with tetanus toxin or BoTx
B (Gansel et al., 1987) or in synaptotagmin I knock-out mice (Geppert et
al., 1994).
REFERENCES
-
Betz W.J. 1970 Depression of transmitter release at the neuromuscular
junction of the frog. J. Physiol. 206, 629-644.
-
Broadie K., Prokop A., Bellen H.J., O'Kane C.J.,
Schulze K.L. and Sweeney S.T. 1995 Syntaxin and synaptobrevin
function downstream of vesicle docking in Drosophila. Neuron 15,
663-73.
-
Brown T.H., Perkel D.H. and Feldman M.W. 1976 Evoked neurotransmitter release:
statistical effects of nonuniformity and nonstationarity. Proc. Natl. Acad.
Sci. USA 73, 2913-2917.
-
Calakos N. and Scheller R.H. 1996 Synaptic vesicle biogenesis, docking
and fusion: a molecular description. Physiol. Reviews 76, 1-29.
-
Ceccarelli B. and Hurlbut W.P. 1980 The vesicle hypothesis of the release
of quanta of acetylcholine. Physiol. Rev. 60, 396-441.
-
Ceccarelli B., Hurlbut W.P. and Mauro A. 1973 Turnover of transmitter and
synaptic vesicles at the frog neuromuscular junction. J. Cell Biol. 57,
499-524.
-
Christensen B.N. and Martin A.R. 1970. Estimates of probability of transmitter
release at the mammalian neuromuscular junction. J. Physiol. 210, 933-945.
-
Courtney K.R. 1978. Extended moment analysis for binomial parameters of
transmitter release. J. Theor. Biol.73, 285-292.
-
Cremona O. and De Camilli P. 1997 Synaptic vesicle endocytosis. Curr. Opin.
Neurobiol. 7, 323-30.
-
DeBello W.M., O'Connor V., Dresbach T., Whiteheart S.W.,
Wang S.S., Schweizer F.E., Betz H., Rothman J.E. and
Augustine G.J. 1995 SNAP-mediated protein-protein interactions essential
for neurotransmitter release. Nature 373, 626-30.
-
Elmqvist D. and Quastel D.M.J. 1965 A quantitative study of end-plate potentials
in isolated human muscle. J. Physiol.178, 505-529.
-
Fesce R. 1990 Stochastic approaches to the study of synaptic function.
Progr. Neurobiol. 35, 85-133.
-
Fesce R., Grohovaz F. Valtorta F. and Meldolesi J. 1994 Neurotransmitter
release: fusion or ‘kiss-and-run’? Trends in Cell Biol. 4, 1-4.
-
Gansel M., Penner R. and Dreyer F. 1987 Distinct sites
of action of clostridial neurotoxins revealed by double-poisoning of mouse
motor nerve terminals. Pflü. Arch., Eur. J. Physiol. 409, 533-539.
-
Ginsborg B.L. and Jenkinson D.H. 1976 Transmission of impulses from nerve
to muscle. In: Neuromuscular junction. Handbook of Experimental Pharmacology,
42, 229-364. (ed. E. Zaimis). Berlin: Springer-Verlag.
-
Heuser J.E. and Reese T.S. 1973 Evidence for recycling of synaptic vesicle
membrane during transmitter release at the frog neuromuscular junction.
J. Cell Biol. 57, 315-344.
-
Hanson P.I., Heuser J.E. and Jahn R. 1997 Neurotransmitter release - four
years of SNARE complexes. Curr. Opin. in Neurobiol. 73, 310-315.
-
Hurlbut W.P., Longenecker H.B. and Mauro A. 1971 Effects of calcium and
magnesium on the frequency of miniature endplate potentials during prolonged
tetanization. J. Physiol. 219, 17-38.
-
Katz B. and Miledi R. 1967 Ionic requirements of synaptic transmitter
release. Nature 215, 651.
-
Liley A.W. and North K.A.K. 1953 An electrical investigation of the effects
of repetitive stimulation on mammalian neuromuscular junction. J. Neurophysiol.
16, 509-527.
-
Llinás R., Sugimori M. and Silver R.B. 1992 Microdomains of
high calcium concentration in a presynaptic terminal. Science 256, 677-679.
-
Mallart A. and Martin A.R. 1967 An analysis of facilitation of transmitter
release at the neuromuscular junction of the frog. J. Physiol. 193, 679-694.
-
Meiri R. and Rahamimoff R. 1978 Clumping and oscillations in evoked
transmitter release at the frog neuromuscular junction. J. Physiol.
278, 513-523.
-
Miyamoto M.D. 1986 Probability of quantal transmitter release from nerve
terminals: theoretical considerations in the determination of spatial variation.
J. Theor. Biol. 123, 289-304.
-
Molgo J., Siegel L.S., Tabti N. and Thesleff S. 1989 A study of synchronization
of quantal transmitter release from mammalian motor endings by the use
of botulinum toxins type A and D. J. Physiol. 411, 195-205.
-
Montecucco C. and Schiavo G. 1995 Structure and function of tetanus and
botulinum neurotoxins. Quart. Rev. Biophys. 28, 423-472.
-
Palfrey H.C. and Artalejo C.R. 1998. Vesicle recycling revisited: rapid
endocytosis may be the first step. Neuroscience 83, 969-989.
-
Sacchi O., Rossi M.L., Canella R. and Fesce R. 1998 Synaptic current at
the rat ganglionic synapse ant its interaction with the neuronal voltage-dependent
currents. J. Neurophysiol. 79, 727-742.
-
Stevens C.F. and Wang Y. 1995 Facilitation and depression at single central
synapses. Neuron 14, 795-802.
-
Thies R.E. 1965 Neuromuscular depression and apparent depletion of transmitter
in mammalian muscle. J. Neurophysiol. 128, 427-442.
-
Wu M.N. and Bellen H.J. 1997 Genetic dissection of synaptic transmission
in Drosophila. Curr. Opin. Neurobiol. 7, 624-630.

 0
0







